A variable line passing through point P(2,1) meets the axes at A and B . Find the locus of the circumcenter of triangle OAB (where O is the origin).
The correct Answer is:x+2y−2xy=0
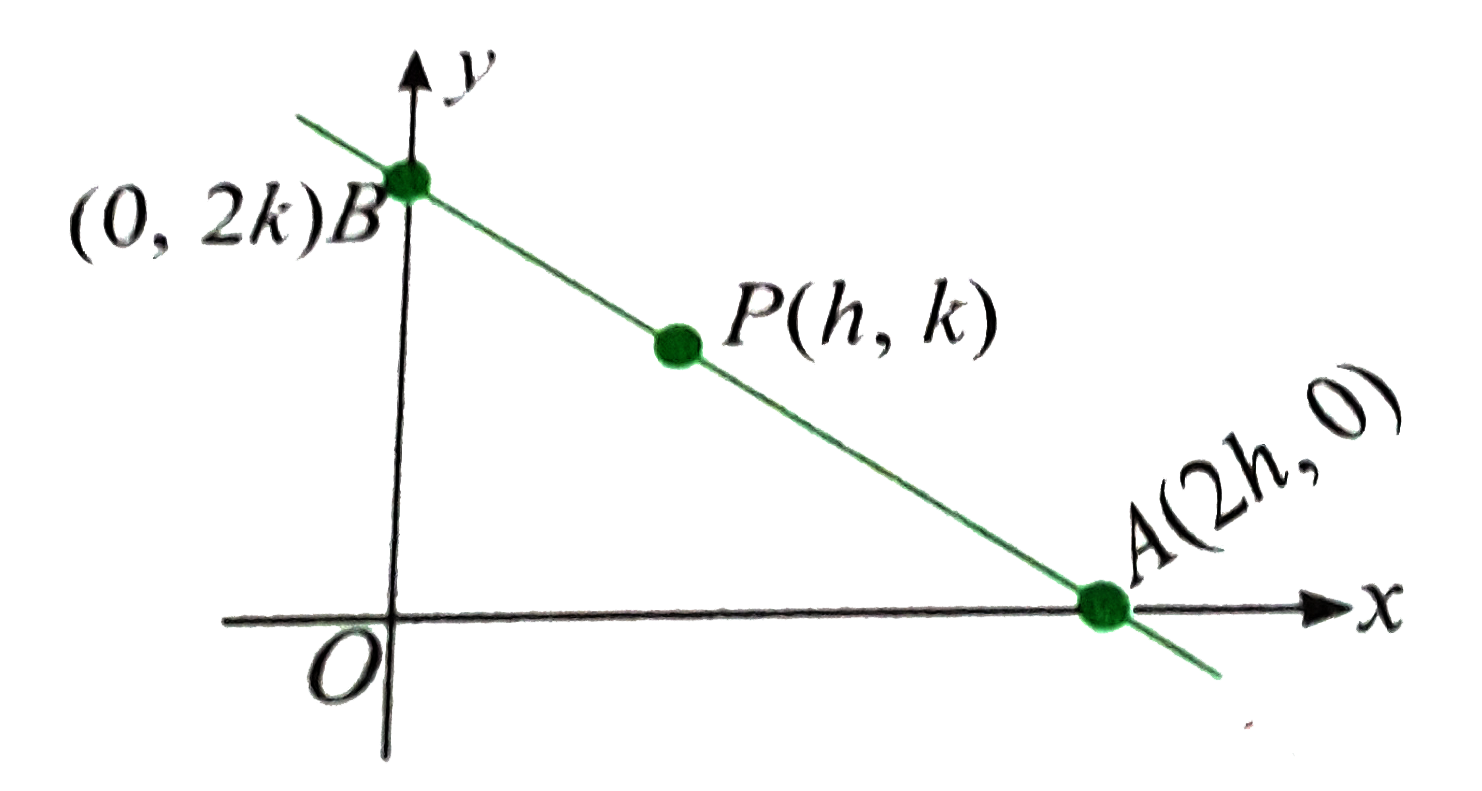
Since triangle OAB is right-angled, its circumcenter is the midpoint of hypotenuse AB.
So, let the midpoint of AB be Q(h,k).
Then the coordinates of A and B are (2h,0) and (0,2h) respectively. Now, points A,B and P are collinear. Therefore, ∣∣
∣
∣
∣∣2h02102k2h0∣∣
∣
∣
∣∣=0
or 2h+4k−4hk=0
or x+2y−2xy=0
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Exercises
59 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.5
5 Videos
- COORDINATE SYSTEMBOOK - CENGAGE ENGLISHCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE ENGLISHCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
A variable line through the point P(2,1) meets the axes at A an d B . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionA circle of radius r passes through the origin and meets the axes at A and B. The locus of the centroid of △OAB is
View SolutionA straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
View SolutionA circle of radius 'r' passes through the origin O and cuts the axes at A and B,Locus of the centroid of triangle OAB is
View SolutionA variable plane passes through a fixed point (a,b,c) and meets the axes at A,B,andC. The locus of the point commom to the planes through A,BandC parallel to the coordinate planes is
View SolutionA variable line y=mx−1 cuts the lines x=2y and y=−2x at points AandB . Prove that the locus of the centroid of triangle OAB(O being the origin) is a hyperbola passing through the origin.
View SolutionA circle passes through origin and meets the axes at A and B so that (2,3) lies on ¯¯¯¯¯¯AB then the locus of centroid of ΔOAB is
View SolutionA line is drawn passing through point P(1,2) to cut positive coordinate axes at A and B . Find minimum area of ΔPAB.
View SolutionA variable plane passes through a fixed point (a,b,c) and cuts the coordinate axes at points A,B,andC. Show that eh locus of the centre of the sphere OABCisax+by+cz=2.
View SolutionA circle of radius 1 unit touches the positive x-axis and the positive y-axis at A and B , respectively. A variable line passing through the origin intersects the circle at two points D and E . If the area of triangle DEB is maximum when the slope of the line is m, then find the value of m−2
View Solution
