A vertex of an equilateral triangle is 2,3 and the opposite side is x+y=2. Find the equations of other sides.
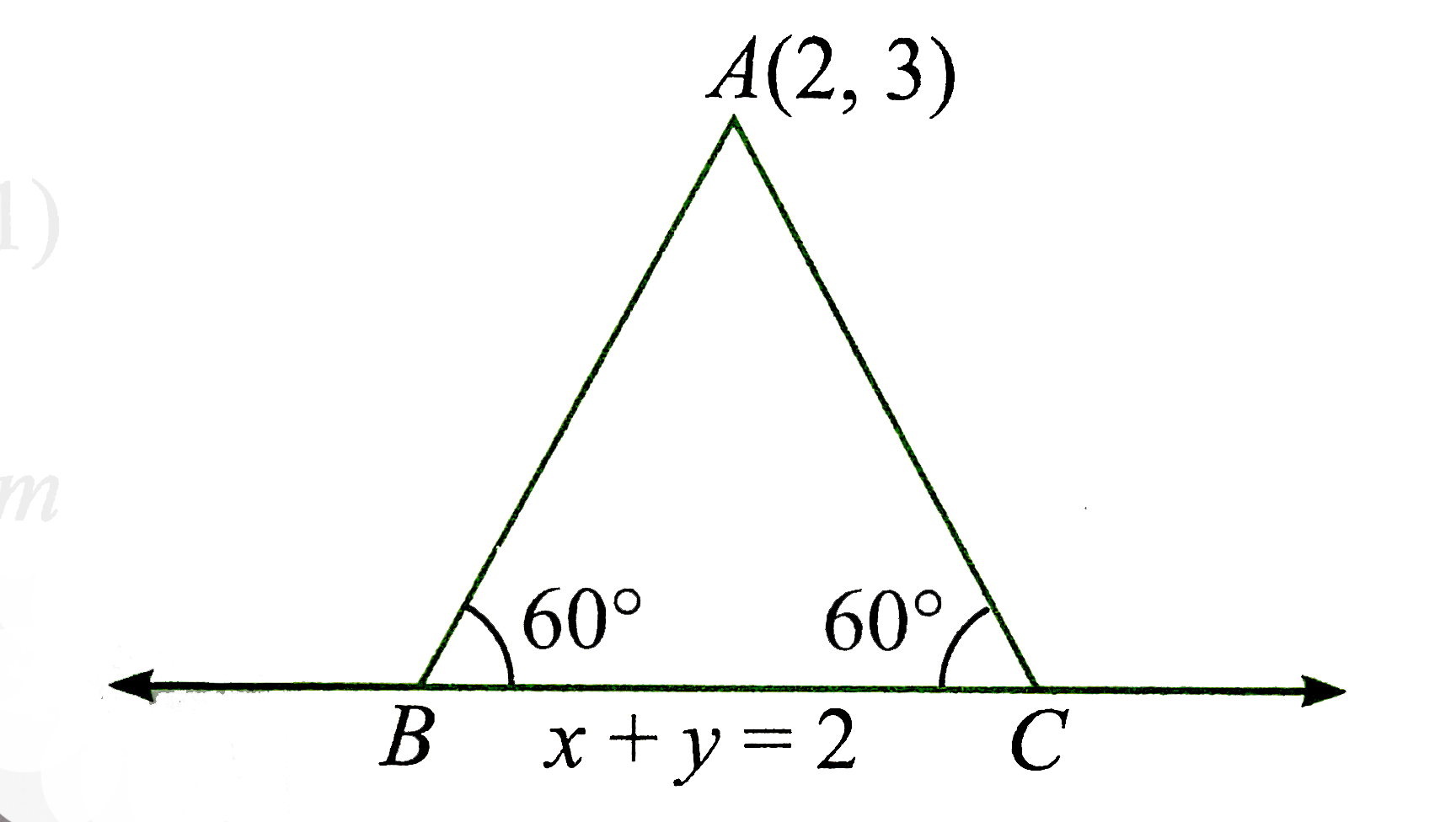
Given line is
x+y−2=0 (1)
Its slope is m1=−1
Let the slope of the line be m which makes an angle of 60∘ with line in (1). Then,
tan60∘=∣∣∣m1−m1+m1m∣∣∣ or √3=∣∣∣−1−m1−m∣∣∣
or √3=∣∣∣1+mm−1∣∣∣ or 1+mm−1=±√3
or 1+m=±√3(m−1)
or m=√3+1√3−1,√3−1√3+1
=2+√3,2−√3
Therefore, the equations of other two sides of the triangle are
y−3=(2+√3)(x−2)
and y−3=(2−√3)(x−2)
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
FIITJEE CHAPTER PRACTICE PROBLEM STRAIGHT LINE 2 L I M I T E D 6 1 Each side of a square is of length 6 units and the centre of the is (-1, 21, One of square diagonals is parallel to y 0 Find the co-ordinates of the square l 2 A vertex of an equilateral triangle is (2, 3) and the opposite side is x y 2. Find the equation of other sides 3 Aline passes through the point P(2, 3 and makes an angle u with postive direction ot xais If it meets the lines represented by x -2xy -y o at the points A and B PAPB e 0, x] then number of such equal io 4 If the slopes of the lines given by the equation 24x ax y+26xy 3 ular distance oint (1, 1) from these the values of
View SolutionA vertex of an equileteral triangle is (2;3) and the equation of the opposite sides is x+y=2 .Find the equation of the other sides of triangle .
View Solution
Knowledge Check
A vertex of an equateral triangle is (2,3) and the opposite side is x + y =2. The equaiton of other sides are
A(2±√3)x−y=1±2√3B(2±√3)x+y=1±2√3C(1±2√3)x−y=2±√3D(2±√3)x+y=1±2√3The vertex of an equilateral triangle is (2,−1) and the equation of its base is x+2y=1. The length of its sides is
A4√15B2√15C43√3D1√5
One vertex of an equilateral triangle is (2,3) and the equation of one side is x−y+5=0. Then the equations to other sides are
View SolutionThe vertex of an equilateral triangle is (2,3) and the equation of the opposite side is x+y=2. Then, the other two sides are y−3=(2±√3)(x−2).
View SolutionThe vertex of an equilateral triangle is (2,3) and the equation of the opposite side is x+y=2. Then, the other two sides are y−3=(2±√3)(x−2).
View SolutionThe vertex of an equilateral triangle is (2,3) and the equation of the opposite side is x+y=2. Then, the other two sides are y−3=(2±√3)(x−2).
View SolutionThe co-ordinates of the vertex of an equilateral triangle are (2,−1) and equation of its base is x+y−1=0. Find the equations of its other two sides.
View SolutionThe co-ordinates of the vertex of an equilateral triangle are (2,−1) and equation of its base is x+y−1=0. Find the equations of its other two sides.
View Solution
