Question

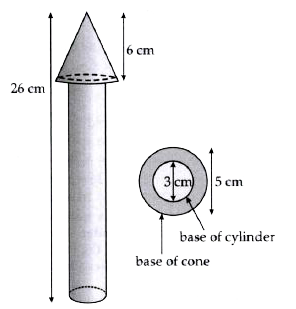
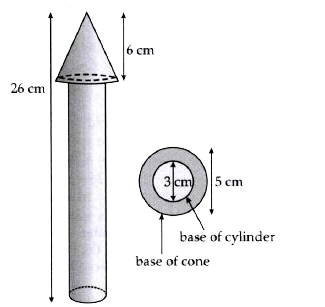
A wooden toy rocket is in the shape of a cone mounted on a cylinder. The height of the entire rocket is 26 cm, while the height of the conical part is 6 cm. The base of the conical portion has a diameter of 5 cm, while the base diameter of the cylindrical portion is 3 cm. If the conical portion is to be painted orange and the cylindrical portion yellow, find the area of the rocket painted with each of these colours.

Explanation

To solve the problem of finding the surface area of the wooden toy rocket, which consists of a conical part and a cylindrical part, we will follow these steps:

Step 1: Identify the dimensions of the rocket
- Height of the entire rocket = 26 cm
- Height of the conical part = 6 cm
- Therefore, the height of the cylindrical part = 26 cm - 6 cm = 20 cm
- Diameter of the conical base = 5 cm, thus radius (R) = 5/2 = 2.5 cm
- Diameter of the cylindrical base = 3 cm, thus radius (r) = 3/2 = 1.5 cm

Step 2: Calculate the surface area of the cylindrical part
The surface area of the cylindrical part consists of the curved surface area and the area of the base.

- Curved Surface Area (CSA) of the cylinder:
\( \text{CSA} = 2 \pi r h = 2 \times \frac{22}{7} \times 1.5 \times 20 \)
\( = 2 \times \frac{22}{7} \times 1.5 \times 20 = \frac{660}{7} \approx 94.29 \text{ cm}^2 \)

- Area of the base of the cylinder:
\( \text{Base Area} = \pi r^2 = \frac{22}{7} \times (1.5)^2 = \frac{22}{7} \times \frac{9}{4} = \frac{198}{28} = 7.07 \text{ cm}^2 \)

- Total Surface Area of the cylindrical part:
\( \text{Total Area (Yellow)} = \text{CSA} + \text{Base Area} = 94.29 + 7.07 = 101.36 \text{ cm}^2 \)

Step 3: Calculate the surface area of the conical part
The surface area of the conical part consists of the curved surface area and the area of the base.

- Curved Surface Area (CSA) of the cone:
To find the slant height (l) of the cone:
\( l = \sqrt{R^2 + h^2} = \sqrt{(2.5)^2 + (6)^2} = \sqrt{6.25 + 36} = \sqrt{42.25} \approx 6.5 \text{ cm} \)

Now, calculate the CSA:
\( \text{CSA} = \pi R l = \frac{22}{7} \times 2.5 \times 6.5 \)
\( = \frac{22 \times 2.5 \times 6.5}{7} = \frac{357.5}{7} \approx 51.07 \text{ cm}^2 \)

- Area of the base of the cone:
\( \text{Base Area} = \pi R^2 = \frac{22}{7} \times (2.5)^2 = \frac{22 \times 6.25}{7} = \frac{137.5}{7} \approx 19.64 \text{ cm}^2 \)

- Total Surface Area of the conical part:
\( \text{Total Area (Orange)} = \text{CSA} + \text{Base Area} = 51.07 + 19.64 = 70.71 \text{ cm}^2 \)

Final Answer
- Area painted orange (conical part) = 70.71 cm²
- Area painted yellow (cylindrical part) = 101.36 cm²