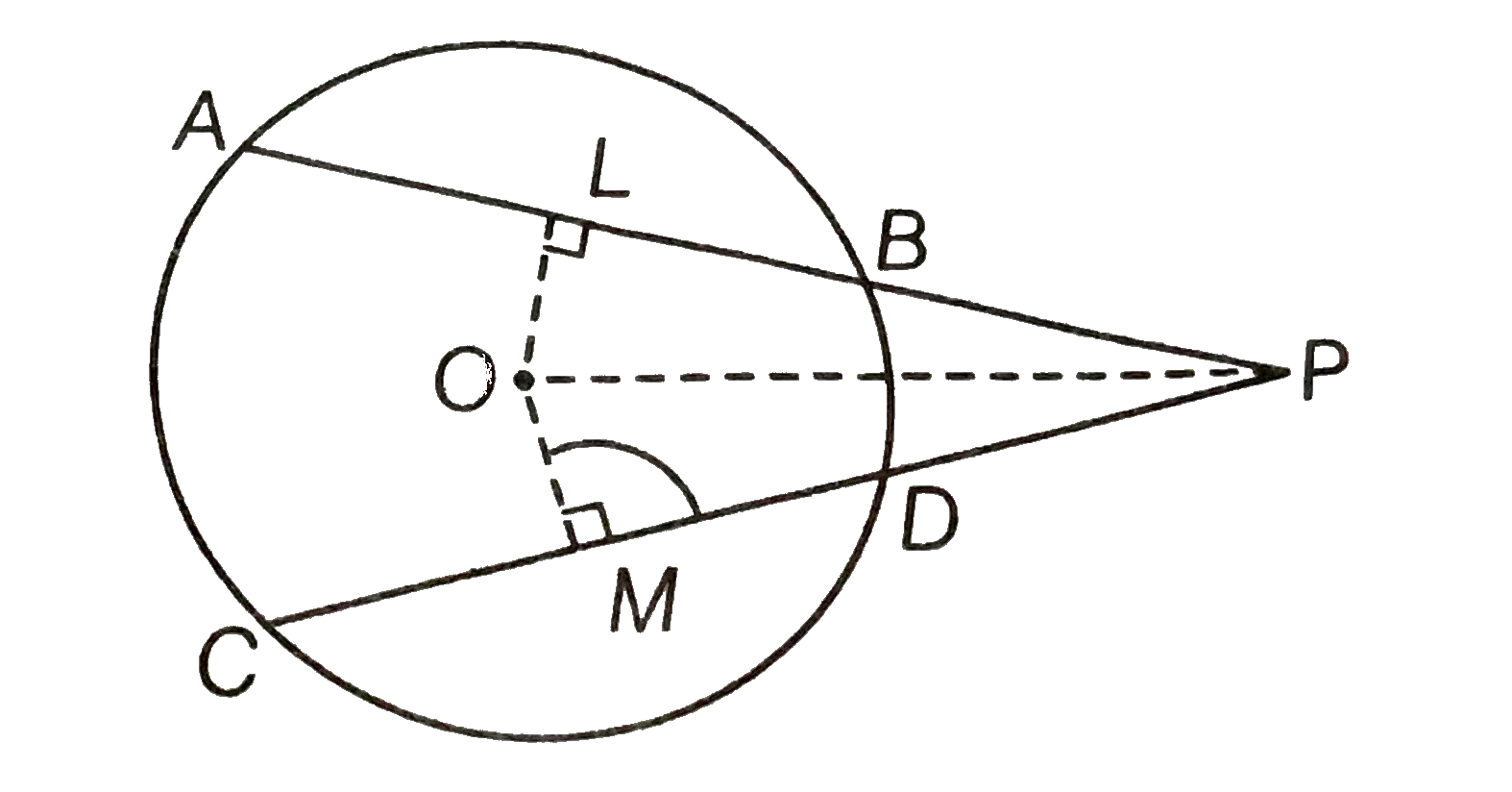
ABandCD are equal chords of a circle whose centre is O, when produced these chords meet at E,Prove that EB=ED.
Given Two equal chords AB and CD of a circle intersecting at a point P.
To prove PB=PD
Construction Join OP, draw OL⊥ABandOM⊥CD
Proof We have, AB=CD
⇒OL=OM
[equal chords are equidistant from the centre]
In ΔOLPandΔOMP,OL=OM [proved above]
∠OLP=∠OMP[each 90∘]
and OP=OP [common side]
∴ΔOLP≅ΔOMP [by RHS congruence rule]
⇒LP=MP [by CPCT] ...(i)
Now, AB=CD
⇒12(AB)=12(CD) [dividing both sides by 2]
⇒BL=DM ..(ii)
[perpendicular drawn from centre to the circle bisects the chord i.e., AL = LB and CM =MD]
On subtracting Eq. (ii) fromEq. (i), we get
LP−BL=MP−DM⇒PB=PD
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
In AB and CD are two equal chords of a circle with center O. OP and OQ are perpendiculars on chords AB and CD respectively. If ∠POQ=150∘ then ∠APQ is equal to
A30∘B75∘C15∘D60∘
AB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD
View SolutionAB and CD are equal and parallel chords of a circle with centre O. Then AC passes through the centre O. [Agree / Disagree]
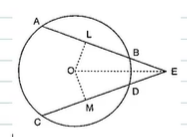
View SolutionTwo equal chords AB and CD of a circle with centre O , when produced meet at a point E, as shown in Figure, Prove that BE=DE and AE=CE.
View SolutionIn Figure, AB and AC are two equal chords of a circle whose centre is O. If OD ⊥AB and OE ⊥AC, prove that ADE is an isosceles triangle.
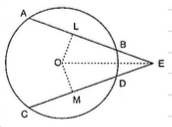
View SolutionTwo equal chords AB and CD of a circle with centre O, when produced meet at a point E, as shown in Figure. Prove that BE=DE and AE=CE.
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionAB and CD are equal and parallel chords of a circle with centre O. Then AC passes through the centre O. [Agree / Disagree]
View Solution
