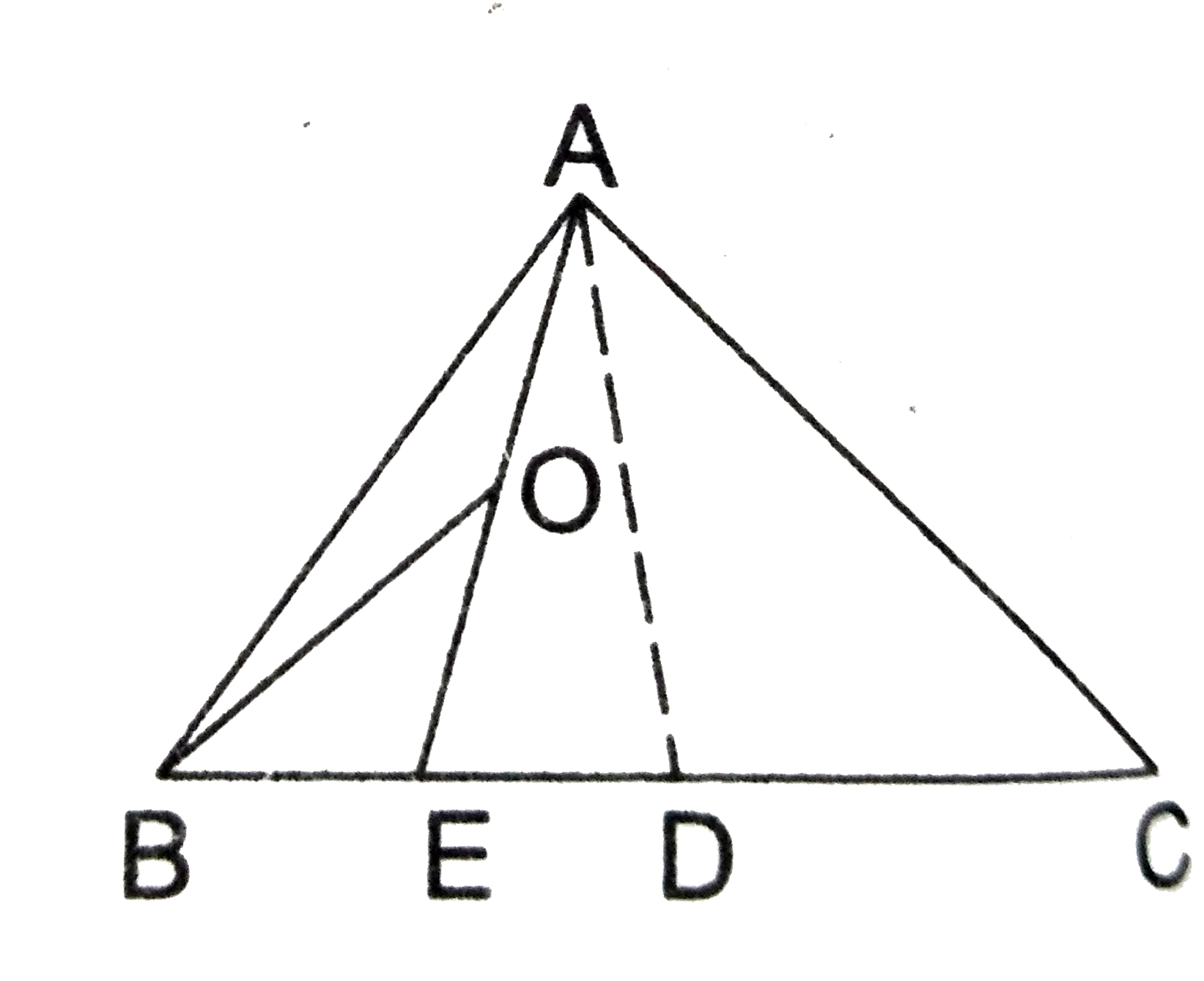
ABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).

Given : A △ABC in which D is the midpoint of BC and E is the important of AD.
To PROVE : ar(△BED)=14ar(△ABC).
Proof : D is the midpoint of BC ⇒ AD is a median of △ ABC
⇒ar(△ABD=ar(△ACD)
[∴ a median divides a △ into two △ of equal area].
⇒ar(△ABD)=12ar(△ABC). ...(i)
E is the midpoint of AD ⇒ BE is a median of △ ABD
⇒ar(△BED)=ar(△BEA)
[∴ a median divides a △ into two △ of equal area].
⇒ar(△BED)=12ar(△ABD)=12{12ar(△ABC)} [using (i)]
⇒ar(△BED)=14ar(△ABC).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
In △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
 A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
The vertex A of △ABC is joined to a point D on the side BC. The midpoint of AD is E.
Prove that ar(△BEC)=12ar(△ABC).
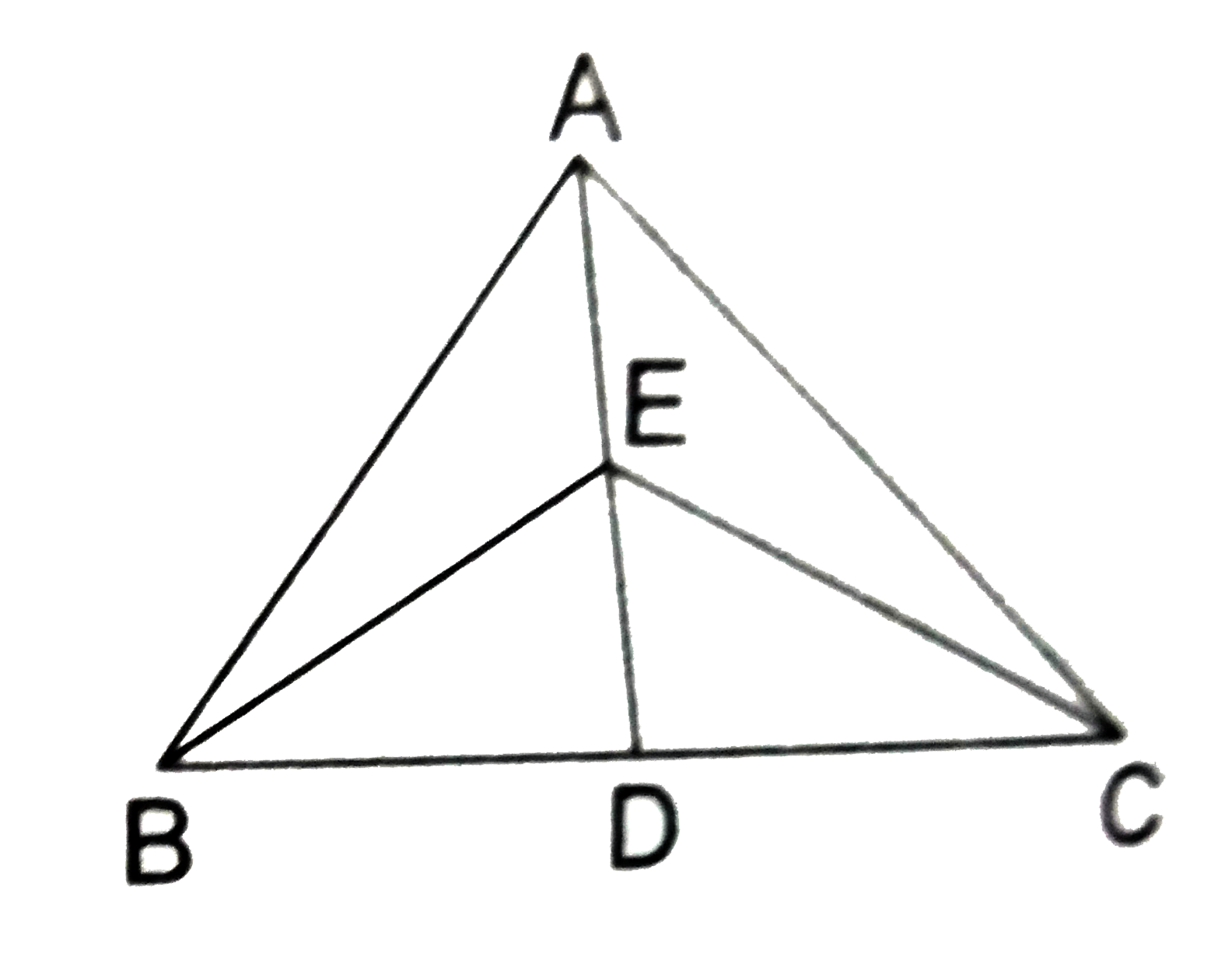
View SolutionIn a ABC,E is the mid-point of median AD. Show that ar(BED)=14ar(ABC)
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED)=14ar (ABC)
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD. Which of the following statements is/are correct?
1. The area of triangle ABC is equal to four times the area of triangle BED.
2. The area of triangle ADC is twice the area of triangle BED.
Select the correct answer using the code given below.
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

View SolutionIn the adjoining figure, BD||CA, E is the midpoint of CA and BD=12CA. Prove that
ar(△ABC)=2ar(△DBC).
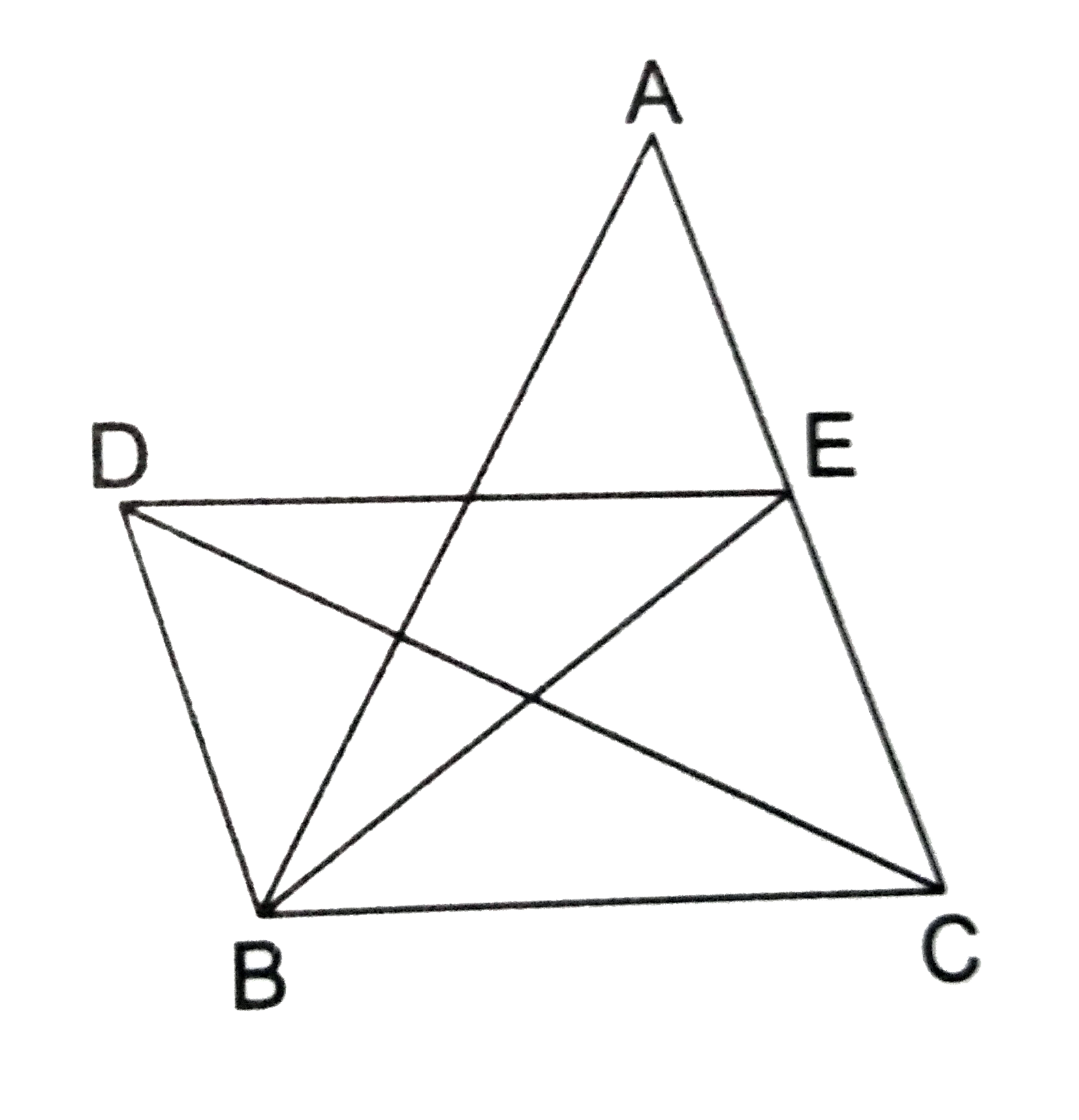
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View Solution