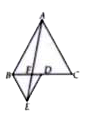
In the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

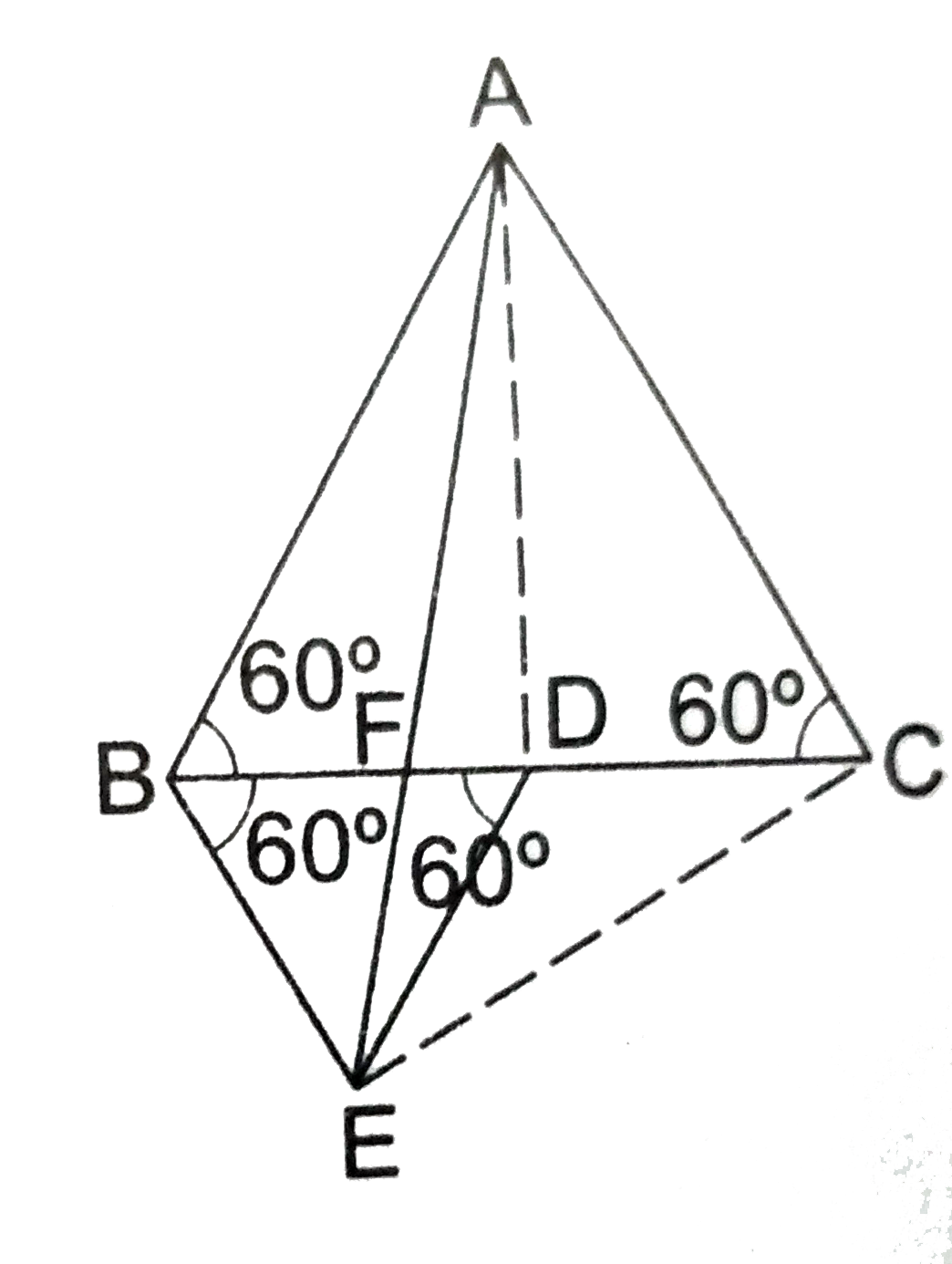
Join AD and EC.
We have ∠ABC=∠DBE=60∘⇒DE||AB
(alt. interior ∠)
and ∠ACB=∠DBE=60∘⇒BE||AC
[∴△ABCand△BDE are eq.△].
Now, let each side of △BDE=a.
Then, ar(△BDE)=√34a2. ...(i)
Each side of △ ABC = 2a " " [∴BC=2BD].
∴ar(△ABC)=√34(2a)2=4(√34a2). ...(ii)
From (i) and (ii), we get
ar(△BDE)=14ar(△ABC). ...(iii)
Now, AD is a median of △ABC
⇒ar(△ABD)=12ar(△ABC). ...(iv)
But, ar(△BAE)=ar(△ABD) ...(v)
[∴ same base AB and same parallels AB and DE].
From (iv) and (v), we get
ar(△BAE)=12ar(△ABC). ...(vi)
From (iii) and (vi), we get
ar(△BDE)=12ar(△BAE). ...(vii)
Now, ar(△BDE)=12ar(△BEC) ...(viii)
[∴ ED is a median of △BEC]
From (iii) and (viii), we get
ar(trianglABC)=2ar(△BEC)...(ix)
Now, ar(△AED)=ar(△BDE)
[∴ same base DE and parallels AB and DE]
⇒ar(△AED)−ar(△FED)=ar(△BDE)−ar(△FED)
⇒ar(△AFD)=ar(△BFE). ...(x)
Now, height of △AFD= height of △ABC=H=√32(2a)=√3a
and height of △FED= height of △BDE=h=√32(a)=√32=H2.
∴ar(△AFD)=12×FD×Handar(△FED)=12×FD×H2
⇒ar(△AFD)=2ar(△FED) ...(ξ)
⇒(trian≥BFE)=2ar(△FED) ...(ξi) [using (x)].
Now, ar(△AFC)=ar(△AFD)+ar(△ADC)
=2ar(△FED)+12{ar(△ABC)} [using (xi)]
=2ar(△FEd)+12{4ar(△BDE)} [using (iii)]
=2ar(△FED)+2{ar(△BFE)+ar(△FED)}
=2ar(△FED)+2{ar(△FED)+ar(△FED)}
[using (xii)]
=8ar(△FED)
⇒ar(△FED)=18ar(△AFC).
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 1138videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)32videos
AREAS OF PARALLELOGRAMS AND TRIANGLES
- BOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)16videos
AREAS OF TRIANGLES AND QUADRILATERALS
Similar Questions
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
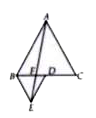
ar(ΔBDE) = 1/4 ar(ΔABC)View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
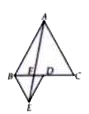
ar(ΔBDE) = 1/2 ar(ΔBAE)View Solution
Knowledge Check
- Question 1 - Select One
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Then, ar(ΔBDE)=12ar(ΔABC).
ATrueBFalseCPartially trueDNone of these
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
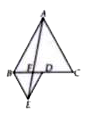
ar(ΔABC) = 2 ar(ΔBEC)View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
ar(ΔBFE) = 2 ar(ΔFED)View SolutionIn the figure, ABC and BDE are two equilateral triangle such that D is the mid-point of BC. If AE intersects BC at F, show that:
(i) ar(ΔBDE)=14ar(ΔABC) (ii) ar(ΔBDE)=12ar(ΔBAE)
(iii) ar(ΔABC)=2ar(ΔBEC) (iv) ar(ΔBFE)=ar(ΔAFD)
(v) ar(ΔBFE)=2ar(ΔFED) (vi) ar(ΔFED)=18ar(ΔAFC)
 View Solution
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).
 View Solution
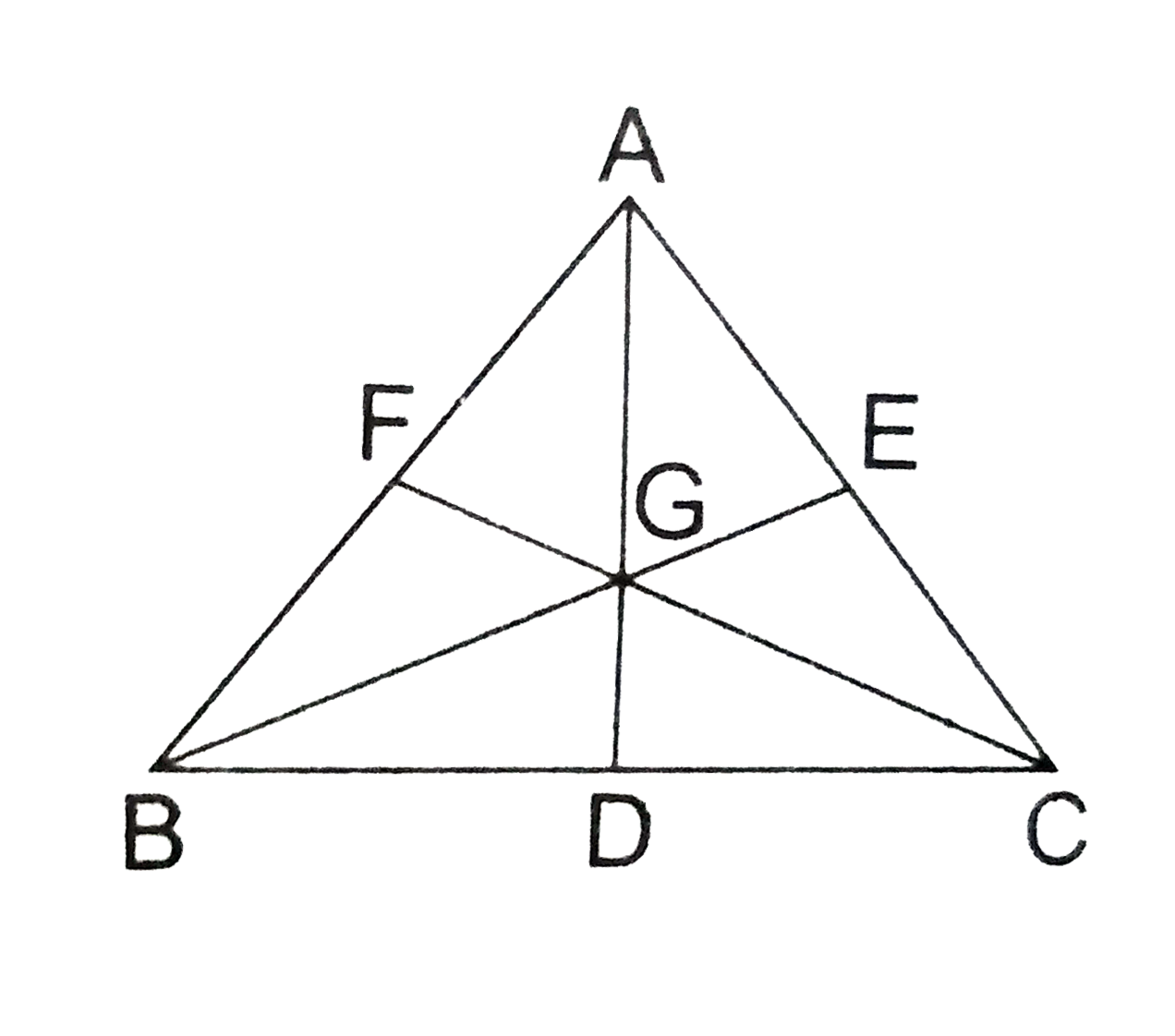
View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
 View Solution
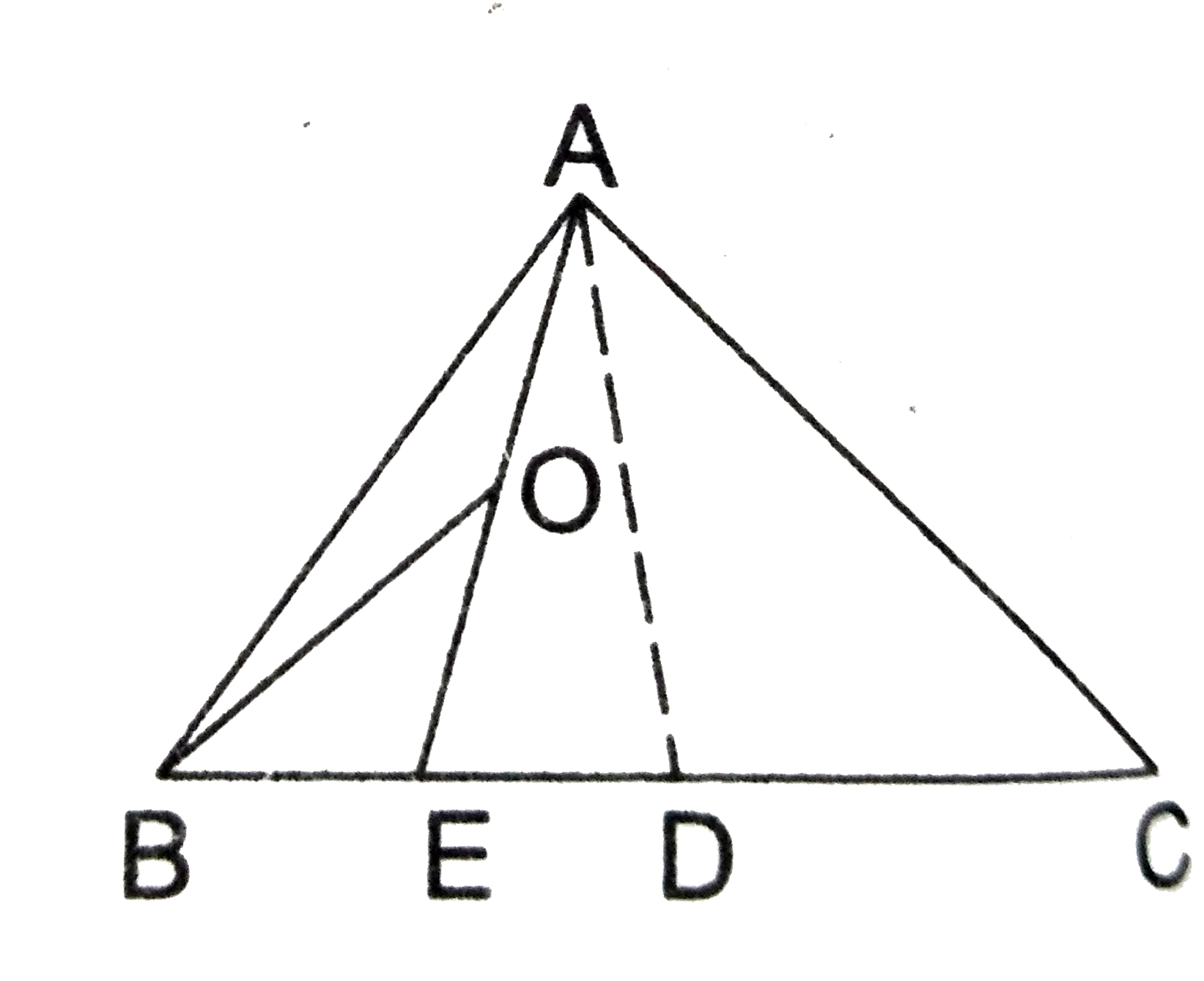
View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
 View Solution
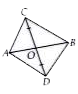
View SolutionIn figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O , show that ar(△ABC)=ar(△ABD).
 View Solution
View Solution

