ABCD is a parallelogram. A circle through A, B is so drawn that it intersects AD at P and BC at Q. Prove that P, Q, C and D are concyclic.
Given ABCD is a parallelogram. A circle whose centre O passes through A, B is so drawm that it intersect AD at P and BC at Q
To prove Points P, Q, C and D are con-cyclic.
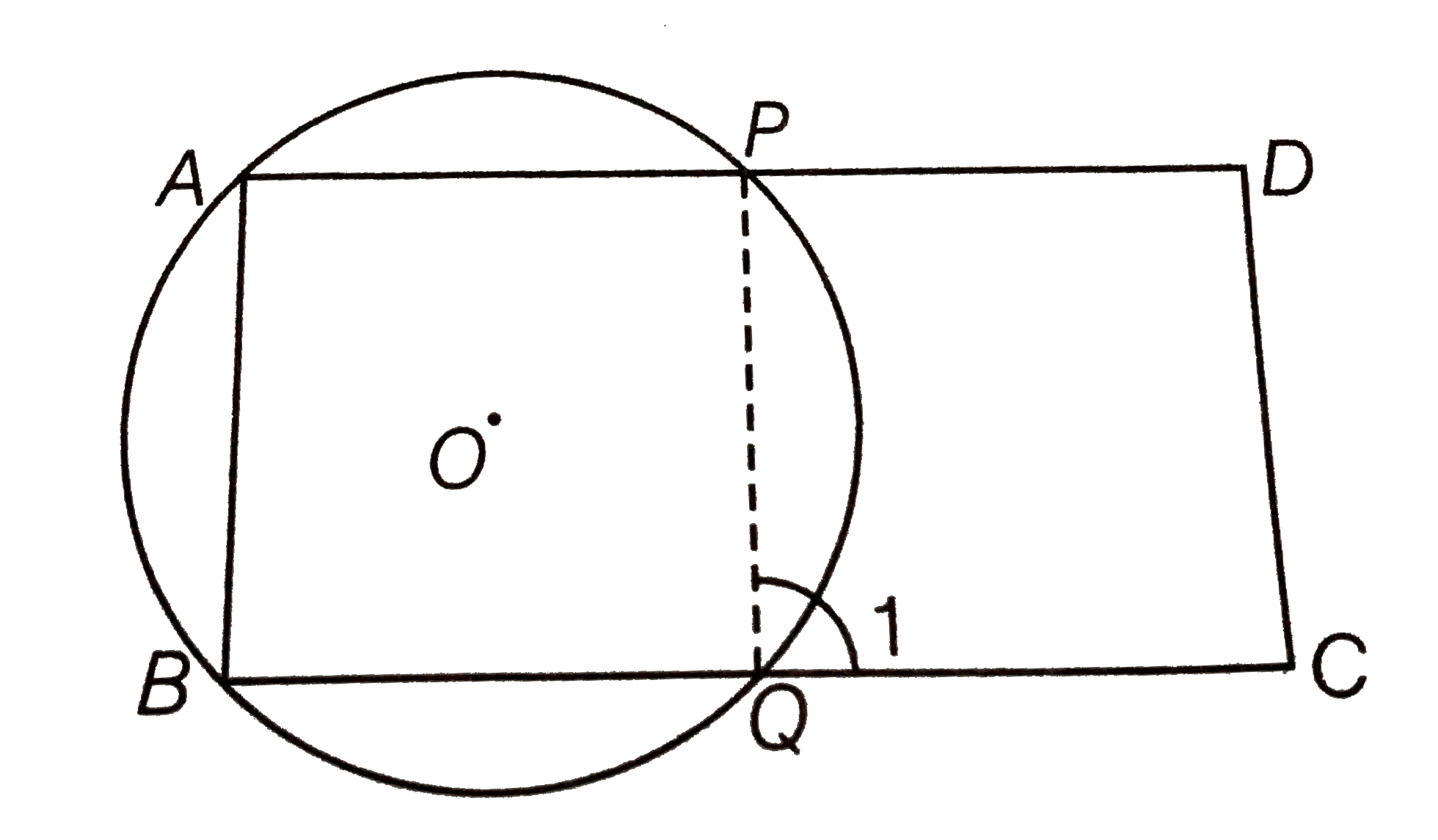
Construction Join PQ
Proof ∠1=∠A [exterior angle property of cyclic quadrilateral]
But∠A=∠C [opposite angles of a parallelogram]
∴∠1=∠C ...(i)
But ∠C=∠D=180∘
[sum of cointerior angles on same side is 180∘]
⇒∠1+∠D=180∘ [from Eq. (i)]
Thus, the quadrilateral QCDP is cyclic.
So, the points P, Q ,C and D are con-cyclic.
Topper's Solved these Questions
Similar Questions
ABCD is a parallelogram. The circle through A, B and C intersect CD (produced ifnecessary) at E. Prove that AE = AD.
View SolutionABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O , a time is drawn to intersect AD at P and BC at Q . Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O , a time is drawn to intersect AD at P and BC at Q . Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View Solution
