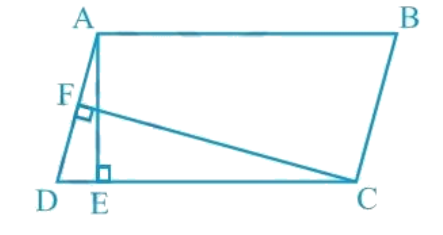
ABCD is a parallelogram, AE⊥DCand CF⊥AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
To solve the problem, we will follow these steps:
Step 1: Write down the given information.
We have:
- AB=16cm
- AE=8cm
- CF=10cm
- AE⊥DC (AE is perpendicular to DC)
- CF⊥AD (CF is perpendicular to AD)
Step 2: Understand the area of the parallelogram.
The area of a parallelogram can be calculated using the formula:
Area=Base×Height
We can calculate the area of parallelogram ABCD using two different bases and their corresponding heights.
Step 3: Calculate the area using base DC.
Using DC as the base and AE as the height:
Area=DC×AE
Since DC=AB (opposite sides of a parallelogram are equal):
DC=16cm
Thus, the area can be expressed as:
Area=16×8=128cm2
Step 4: Calculate the area using base AD.
Now, using AD as the base and CF as the height:
Area=AD×CF
Substituting CF=10cm:
Area=AD×10
Step 5: Set the two area expressions equal to each other.
Since both expressions represent the area of the same parallelogram, we can set them equal:
128=AD×10
Step 6: Solve for AD.
To find AD, we rearrange the equation:
AD=12810=12.8cm
Conclusion:
The length of AD is 12.8cm.
---
We have:
- AB=16cm
- AE=8cm
- CF=10cm
- AE⊥DC (AE is perpendicular to DC)
- CF⊥AD (CF is perpendicular to AD)
The area of a parallelogram can be calculated using the formula:
Area=Base×Height
We can calculate the area of parallelogram ABCD using two different bases and their corresponding heights.
Using DC as the base and AE as the height:
Area=DC×AE
Since DC=AB (opposite sides of a parallelogram are equal):
DC=16cm
Thus, the area can be expressed as:
Area=16×8=128cm2
Now, using AD as the base and CF as the height:
Area=AD×CF
Substituting CF=10cm:
Area=AD×10
Since both expressions represent the area of the same parallelogram, we can set them equal:
128=AD×10
To find AD, we rearrange the equation:
AD=12810=12.8cm
The length of AD is 12.8cm.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.4
8 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - EXERCISE 9.1
1 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - NCERTCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Solved Examples
4 Videos
- CIRCLESBOOK - NCERTCHAPTER - CIRCLESEXERCISE - EXERCISE 10.2
2 Videos
Similar Questions
In Figure, ABCD is a parallelogram, AE ⊥DC and CF⊥AD . If AB=16CM, AE=8cm and CF=10cm, find AD
View SolutionIn fig. 15 ABCD is a parallelogram CM⊥AB and BL⊥AD. If AB=16 cm, AD=12 cm, CM=10 cm, find BL If AD=10cm, CM=8cm, BL=12 cm, find AB .
View SolutionIn Fig.20, ABCD is a parallelogram, DL⊥AB and DM⊥BC. If AB=18 cm , BC=12 cm and DM=9.3 cm, find DL.
View SolutionIn Fig. 21, ABCD is a parallelogram, DL⊥AB. If AB=20 cm , AD=13 cm and area of the parallelogram is 100 cm2 find AL.
View SolutionIn Figure, ABCD is a parallelogram. If AB=12cm,AE=7.5cm,CF=15cm, then AD=

(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If BD=2.5cm, AB=5cm and AC=4.2cm , find DC . (ii) If BD=2cm, AB=5cm and DC=3cm, find AC . (iii) If AB=3.5cm , AC=4.2cm and DC=2.8cm , find BD .
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If AD=5.6cm , BC=6cm and BD=3.2cm , find AC . (ii) If AB=10cm , AC=6cm and BC=12cm , find BD and DC .
View SolutionIn a ABC , AD is the bisector of ∠A , meeting side BC at D . If AB=10cm , AC=14cm and BC=6cm , find BD and DC (ii) If AC=4.2cm , DC=6cm and BC=10cm , find AB . (iii) If AB=5.6cm , AC=6cm and DC=3cm , find BC .
View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View SolutionLet ABCD be a parallelogram and ABEF be a rectangle with EF lying along the line CD . If AB=7cm and BE=6.5cm , then the area of the parallelogram is 11.375cm2 (b) 22.75cm2 (c) 45cm2 (d) 45.5cm2
View Solution
