ABCD is a parallelogram and AC, BD are its diagonals. Show that : −−→AC+−−→BD=2−−→BC,−−→AC−−−→BD=2−−→AB.Solution in Punjabi
Step by step video & image solution for ABCD is a parallelogram and AC, BD are its diagonals. Show that : vec(AC)+vec(BD)=2vec(BC),vec(AC)-vec(BD)=2vec(AB). by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Classify the following physical quantities into scalars and vectors:
9gm03:38View SolutionFind the points on z-axis which are at a distance of √21 from the point (1,2,3).
04:35View SolutionLet ABCD is a parallelogram and →AC,→BD be its diagonal, then →AC+→BD is
02:48View SolutionABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
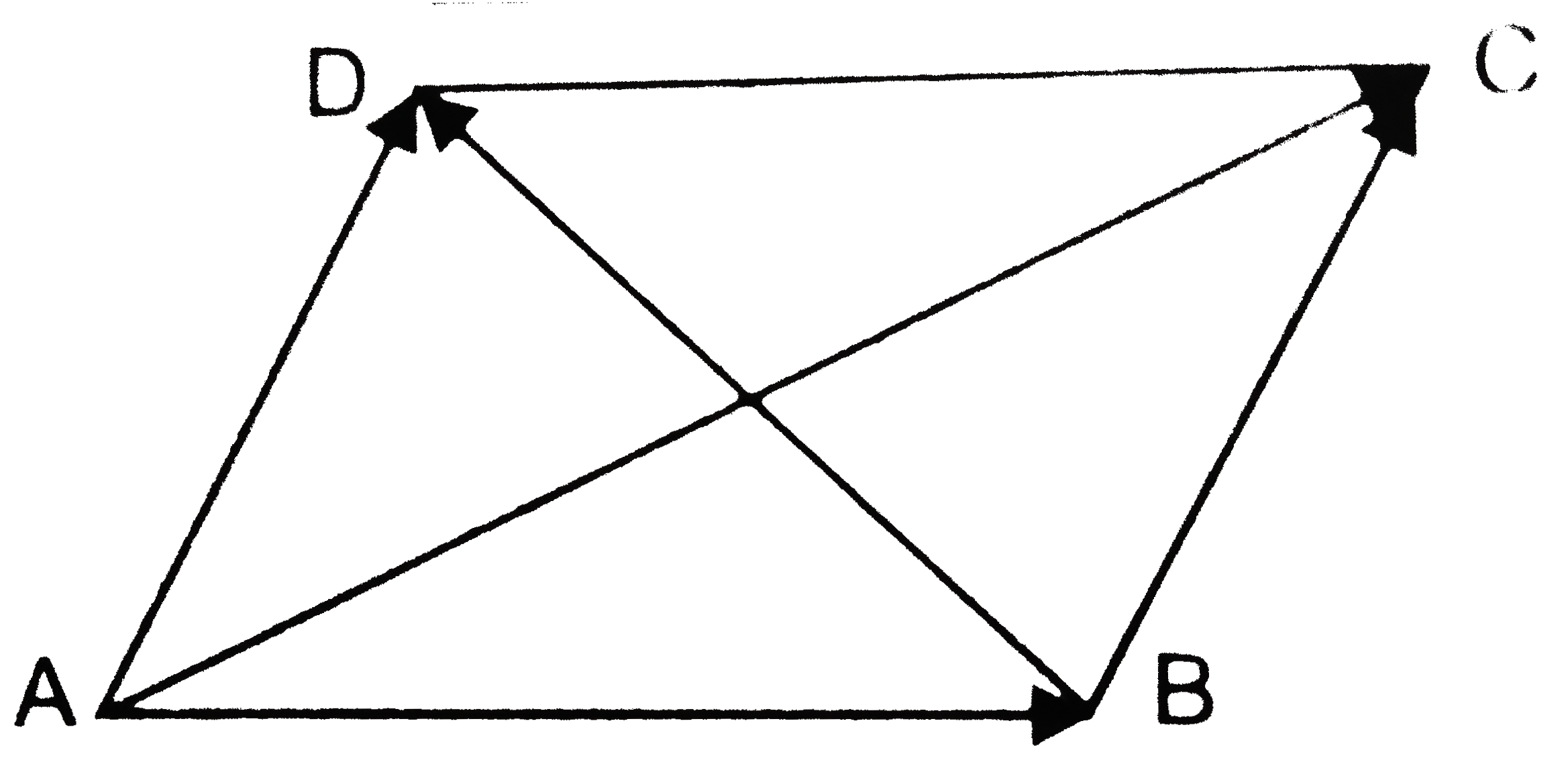 . 02:10View Solution
. 02:10View SolutionA parallelogram ABCD. Prove that −−→AC+−−→BD=2−−→BC'
04:07View SolutionABCD is a parallelogram with AC and BD as diagonals. Then, A→C−B→D=
01:29View SolutionIf ABCD is a parallelogram, then −−→AC−−−→BD=
09:05View SolutionABCD एक चतुर्भुज है और AC और BD इसके विकर्ण हैं । सिद्ध करो कि सदिश −−→AB+−−→DC=−−→AC+−−→DB
06:41View SolutionABCD एक समांतर चतुर्भुज है ।AC और BD इसके विकर्ण है । सिद्ध कीजिए -
−−→AC+−−→BD=2−−→BC
−−→AC−−−→BD=2−−→AB.View SolutionABCD एक समान्तर चतुर्भुज हैं और AC, BD इसके विकर्ण हैं|
(a) −−→AB को −−→AC और −−→BD के रूप में व्यक्त करें| (b) −−→AC को −−→BD के रूप में व्यक्त करें|
साथ ही यह सिद्ध करें कि −−→AC+−−→BD=2−−→BC,−−→AC−−−→BD=2−−→AB03:30View Solutionयदि किसी चतुर्भुज ABCD के विकर्ण AC तथा BD हों तो सिद्ध कीजिए कि
−−→AB+−−→BC=−−→AC02:41View Solution¯¯¯¯¯¯AC and ¯¯¯¯¯¯BD are the diagonals of the parallelogram ABCD. Prove that,
−−→AC+−−→BD=2−−→BC and −−→AC−−−→BD=2−−→AB04:05View SolutionABCD সামান্তরিকের ¯¯¯¯¯¯AC ও ¯¯¯¯¯¯BD হল কর্ণ | প্রমাণ করো যে, −−→AC+−−→BD=2−−→BC এবং −−→AC−−−→BD=2−−→AB |
03:09View SolutionABCD is a parallelogram and AC, BD are its diagonals. Show that :
−−→AC+−−→BD=2−−→BC,−−→AC−−−→BD=2−−→AB.03:47View SolutionABCD एक समांतर चतुर्भुज है तो सिद्ध करो −−→AC+−−→BD=2−−→BC
03:31View Solution−−→ACand−−→BD are the diagonals of a parallelogram ABCD. Prove that
(i)−−→AC+−−→BD−2−−→BC
(ii) −−→AC−−−→BD−2−−→AB04:03View Solution
