ABCD is a parallelogram DP is perpendicular to AB. Given BD=5cm,AP=3cm.and area of ΔADP=6 sq. cm, find the perimeter of ABCD.
The correct Answer is:22 cm
To find the perimeter of the parallelogram ABCD, we can follow these steps:
Step 1: Understand the given information
We have:
- BD=5cm
- AP=3cm
- Area of triangle ADP=6cm2
Step 2: Use the area of triangle formula
The area of triangle ADP can be calculated using the formula:
Area=12×base×height
Here, the base is AP and the height is DP. Therefore, we can write:
6=12×AP×DP
Substituting AP=3:
6=12×3×DP
Step 3: Solve for DP
Multiply both sides by 2:
12=3×DP
Now, divide by 3:
DP=123=4cm
Step 4: Use the Pythagorean theorem to find BP
In triangle BDP, we can apply the Pythagorean theorem:
BD2=BP2+DP2
Substituting the known values:
52=BP2+42
This simplifies to:
25=BP2+16
Now, subtract 16 from both sides:
BP2=25−16=9
Taking the square root:
BP=√9=3cm
Step 5: Find the length of AD
In triangle ADP, we again use the Pythagorean theorem:
AD2=AP2+DP2
Substituting the known values:
AD2=32+42
This simplifies to:
AD2=9+16=25
Taking the square root:
AD=√25=5cm
Step 6: Find the lengths of the sides of the parallelogram
Since AB and DC are opposite sides of the parallelogram, we have:
AB=AP+BP=3+3=6cm
And since AD and BC are also opposite sides:
AD=5cm
Step 7: Calculate the perimeter of the parallelogram
The perimeter P of parallelogram ABCD is given by:
P=AB+BC+CD+DA
Since AB=DC=6cm and AD=BC=5cm:
P=6+6+5+5=22cm
Final Answer
The perimeter of parallelogram ABCD is 22cm.
---
We have:
- BD=5cm
- AP=3cm
- Area of triangle ADP=6cm2
The area of triangle ADP can be calculated using the formula:
Area=12×base×height
Here, the base is AP and the height is DP. Therefore, we can write:
6=12×AP×DP
Substituting AP=3:
6=12×3×DP
Multiply both sides by 2:
12=3×DP
Now, divide by 3:
DP=123=4cm
In triangle BDP, we can apply the Pythagorean theorem:
BD2=BP2+DP2
Substituting the known values:
52=BP2+42
This simplifies to:
25=BP2+16
Now, subtract 16 from both sides:
BP2=25−16=9
Taking the square root:
BP=√9=3cm
In triangle ADP, we again use the Pythagorean theorem:
AD2=AP2+DP2
Substituting the known values:
AD2=32+42
This simplifies to:
AD2=9+16=25
Taking the square root:
AD=√25=5cm
Since AB and DC are opposite sides of the parallelogram, we have:
AB=AP+BP=3+3=6cm
And since AD and BC are also opposite sides:
AD=5cm
The perimeter P of parallelogram ABCD is given by:
P=AB+BC+CD+DA
Since AB=DC=6cm and AD=BC=5cm:
P=6+6+5+5=22cm
The perimeter of parallelogram ABCD is 22cm.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - WARMUP EXERCISE10videos
PERIMETER AND AREA
- BOOK - ICSECHAPTER - PERIMETER AND AREA EXERCISE - EXERCISE 17.115videos
PERIMETER AND AREA
- BOOK - ICSECHAPTER - PERCENTAGE, PROFIT AND LOSSEXERCISE - REVISION EXERCISE26videos
PERCENTAGE, PROFIT AND LOSS
- BOOK - ICSECHAPTER - PROBABILITYEXERCISE - TRY THIS14videos
PROBABILITY
Similar Questions
ABCD is a parallelogram where DE is perpendicular to AB. If BD= 17 cm, AE = 15 cm, and area of ΔADE=60sq. cm, find the perimeter of ABCD.
 View Solution
View SolutionLMNO is a parallelogram where OP is perpenducular to AB. If OM=20cm,LP=9cm, and area of ΔLPO=54sq.cm, find the perimeter of LMNO.
View SolutionPQRS is a parallelogram with ST perpendicular to PQ. Given area of Δ PST = 54 sq.cm, QS = 13 cm, and TQ = 5 cm, find the perimeter of the parallelogram.
View SolutionIn a parallelogram ABCD, point P lies in DC such that DP:PC= 3:2. If area of ΔDPB=30sq. cm, ffind the area of the parallelogram ABCD.
View SolutionIn the figure, given alongside, PB and QA are perpendiculars to the line segment AB. If PO = 6 cm, QO = 9 cm and area of ΔPOB−120cm2. find the area of ΔQOA.
 View Solution
View SolutionIn the figure, ABCDE is a pentagon with BE∣∣CD and BC∣∣DE. BC is perpendicular to CD. AB= 5cm, AE=5cm, BE= 7cm, BC= x-y and CD= x+y. If the perimeter of ABCDE is 27cm. find the value of x and y, given x,y,≠0
View SolutionIn figure, ABCD is a parallelogram, AE perpendicular to DC and CF perpendicular to AD. If AB = 16cm, AE = 8cm and CF = 10cm, Find AD.
View SolutionIn DetlaABC,AD is perpendicular to BC. If AD = 12 cm, area of ΔADB=90sq.cm. and area of DetlaADB: area De≤taADC=2:3, find BD and DC.
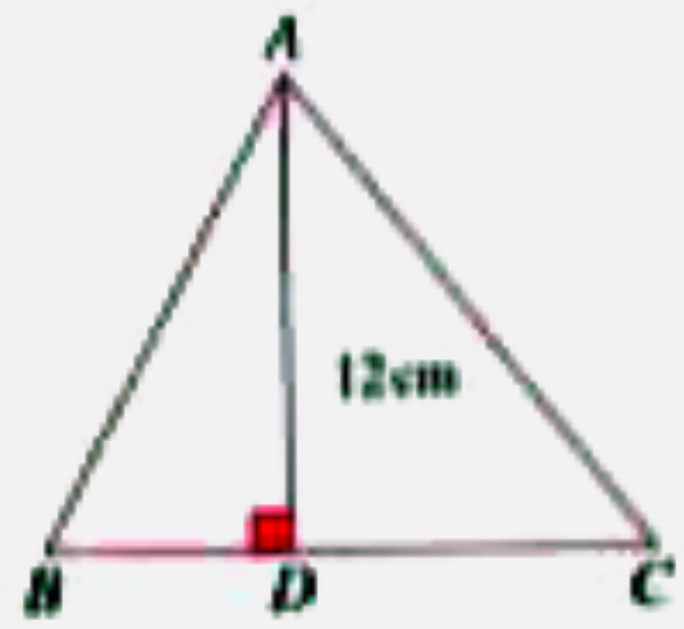 View Solution
View SolutionABCD is a parallelogram of area 162 sq. Cm P is a point on AB such that AP : PB = 1 :2
Calculate
The area of ΔAPDView SolutionThe given figure shows a parallelogram ABCD. E is a point in AD and CE produced meets BA produced at point F. If AE = 4 cm, AF = 8 cm and AB = 12 cm, find the perimeter of the parallelogram ABCD.
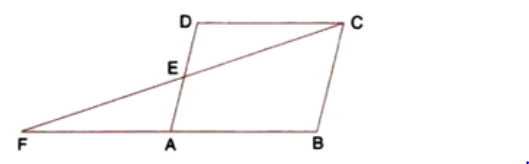 View Solution
View Solution

