ABCD is a parallelogram. Using vector method prove that line joing A and the mid -point of BC intersects the diagonal BD in the ratio 1:2.
The correct Answer is:1:2
Topper's Solved these Questions
- VECTORS BOOK - ARIHANT PRAKASHANCHAPTER - VECTORS EXERCISE - TOPIC TEST 1
16 Videos
- VECTORS BOOK - ARIHANT PRAKASHANCHAPTER - VECTORS EXERCISE - TOPIC -2 (PRACTICE QUESTIONS) (1 MARK QUESTIONS)
34 Videos
- VECTORS BOOK - ARIHANT PRAKASHANCHAPTER - VECTORS EXERCISE - CHAPTER TEST (6 MARK QUESTIONS)
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - ARIHANT PRAKASHANCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - CHAPTER TEST
24 Videos
- VERY SIMILAR TEST 1 BOOK - ARIHANT PRAKASHANCHAPTER - VERY SIMILAR TEST 1 EXERCISE - Section C
10 Videos
Similar Questions
ABCD is a parallelogram. E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC at G, P and H respectively. Prove that : GP=PH
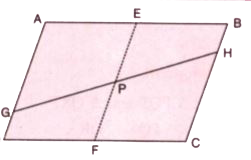
View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionABCD is a parallelogram. E and F are mid-point of side AB and CD respectively. AF and CE intersect diagonal BD at P & Q respectively. If BD = 15 cm, find PQ.

View SolutionIn parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionBy vector method, prove that if the diagonals of a parallelogram intersect perpendicularly,then the parallelogram is rombus.
View SolutionGiven a parallelogram ABCD with area 12 sq. units. A straight line is drawn through the midpoint M of the side BC and the vertex A which cuts the diagonal BD at a point'O'. Use vectors to determine the area of the quadrilateral OMCD.
View SolutionABCD is a parallelogram and E is a point, on BC. If the diagonal BD intersects AE at F, prove that AF×FB×EF×FD.
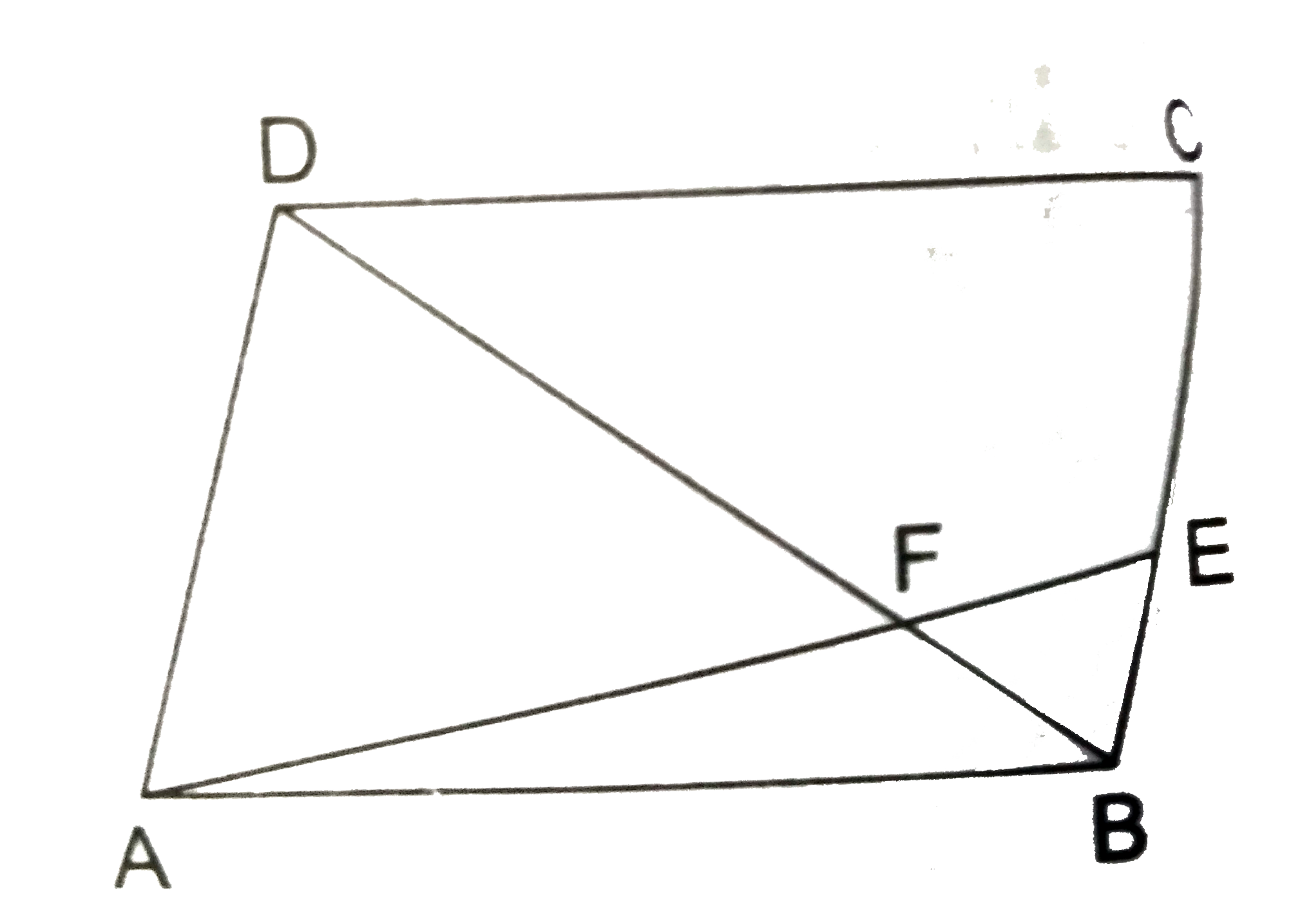
View SolutionGiven Parallelogram ABCD in which diagonals AC and BD at M.Prove M is mid-point of LN.
View Solution
