Given a parallelogram ABCD with area 12 sq. units. A straight line is drawn through the midpoint M of the side BC and the vertex A which cuts the diagonal BD at a point'O'. Use vectors to determine the area of the quadrilateral OMCD.
Step by step video & image solution for Given a parallelogram ABCD with area 12 sq. units. A straight line is drawn through the midpoint M of the side BC and the vertex A which cuts the diagonal BD at a point'O'. Use vectors to determine the area of the quadrilateral OMCD. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Given Parallelogram ABCD in which diagonals AC and BD at M.Prove M is mid-point of LN.
View SolutionThe area of a triangle ABC is 63 sq. units. Two parallel lines DE, FG, are drawn such that they divide the line segments AB and BC into three equal parts. What is the area of the quadrilateral DEGF ?
View Solution
Knowledge Check
The base of an isosceles triangle measures 4 units base angle is equal to 45∘. A straight line cuts the extension of the base at a point M at the angle θ and bisects the lateral side of the triangle which is nearest to M.
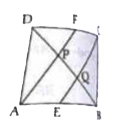
The area of quadrilateral which the straight line cuts off from the given triangle isA3+tanθ1+tanθB3+5tanθ1+tanθC3+tanθ1−tanθD3+2tanθ1+tanθABCD is a parallelogram with base AB = 12 cm and height 5 cm. If E and F are respectively midpoint of AB and CD and diagonal BD intersects AF and CE respectively at P and Q then area of quadrilateral PQCF is
A12 cm2B18 cm2C20 cm2D15 cm2
The base of an isosceles triangle measures 4 units base angle is equal to 45∘. A straight line cuts the extension of the base at a point M at the angle θ and bisects the lateral side of the triangle which is nearest to M.
The area of quadrilateral which the straight line cuts off from the given triangle is
View SolutionIn a parallelogram ABCD, points E and F are respectively midpoint of sides AB and CD (see the adjacent figure). Prove that line segment AF and EC trisect diagonal BD.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionThe diagonals of a parallelogram ABCD intersect at a point O. Through O, a line a drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
View SolutionABCD is a square of side a. A line parallel to the diagonal BD at a distance x from the vertex A cuts the two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x.
View SolutionABCD is a square of side a. A line parallel to the diagonal BD at a distance x from the vertex A cuts the two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x.
View Solution
