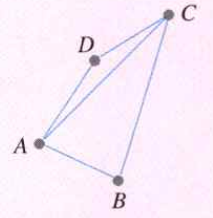
ABCD is a quadrilateral in which AB||DC and AD = BC. Prove that ∠A=∠Band∠C=∠D.
To prove that in quadrilateral ABCD, where AB is parallel to DC and AD = BC, we have angle A = angle B and angle C = angle D, follow these steps:
Step 1: Draw the Quadrilateral
Draw quadrilateral ABCD such that AB is parallel to DC and AD = BC.
Step 2: Extend Line AB
Extend line AB to a point E, making sure that the extension is straight.
Step 3: Draw Parallel Line
Draw line CE parallel to AD. This is a crucial construction that will help us use properties of parallel lines.
Step 4: Identify Given Information
From the problem, we know:
- AD = BC (given)
- AB || DC (given)
Step 5: Use Properties of Parallel Lines
Since AB is parallel to DC and AD is parallel to CE, we can use the property of co-interior angles:
- Angle A + Angle E = 180° (co-interior angles on the same side of the transversal AD)
Step 6: Express Angle A
From the above property, we can express angle A:
- Angle A = 180° - Angle E
Step 7: Establish Parallelogram
Since AD is parallel to CE and AD = CE (as AD = BC and BC = CE), quadrilateral AECD is a parallelogram. Thus, we have:
- AD = CE (opposite sides of a parallelogram)
Step 8: Use Isosceles Triangle Properties
In triangle BCE, since CE = BC (as established), triangle BCE is isosceles. Therefore:
- Angle CBE = Angle CEB (opposite angles of equal sides)
Step 9: Express Angle B
Using the triangle angle sum property in triangle BCE:
- Angle B + Angle CBE + Angle CEB = 180°
- Thus, Angle B = 180° - Angle CBE
Step 10: Compare Angles
From Step 6, we have:
- Angle A = 180° - Angle E
And from Step 9:
- Angle B = 180° - Angle CBE
Since Angle E = Angle CBE (as they are corresponding angles), we can conclude:
- Angle A = Angle B
Step 11: Prove Angle C = Angle D
Since AECD is a parallelogram, we know:
- Angle A + Angle D = Angle B + Angle C
Substituting Angle A = Angle B into the equation gives:
- Angle D = Angle C
Conclusion
Thus, we have proved that:
- Angle A = Angle B
- Angle C = Angle D
Draw quadrilateral ABCD such that AB is parallel to DC and AD = BC.
Extend line AB to a point E, making sure that the extension is straight.
Draw line CE parallel to AD. This is a crucial construction that will help us use properties of parallel lines.
From the problem, we know:
- AD = BC (given)
- AB || DC (given)
Since AB is parallel to DC and AD is parallel to CE, we can use the property of co-interior angles:
- Angle A + Angle E = 180° (co-interior angles on the same side of the transversal AD)
From the above property, we can express angle A:
- Angle A = 180° - Angle E
Since AD is parallel to CE and AD = CE (as AD = BC and BC = CE), quadrilateral AECD is a parallelogram. Thus, we have:
- AD = CE (opposite sides of a parallelogram)
In triangle BCE, since CE = BC (as established), triangle BCE is isosceles. Therefore:
- Angle CBE = Angle CEB (opposite angles of equal sides)
Using the triangle angle sum property in triangle BCE:
- Angle B + Angle CBE + Angle CEB = 180°
- Thus, Angle B = 180° - Angle CBE
From Step 6, we have:
- Angle A = 180° - Angle E
And from Step 9:
- Angle B = 180° - Angle CBE
- Angle A = Angle B
Since AECD is a parallelogram, we know:
- Angle A + Angle D = Angle B + Angle C
- Angle D = Angle C
Thus, we have proved that:
- Angle A = Angle B
- Angle C = Angle D
Topper's Solved these Questions
- QUADRILATERALS BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS
10 Videos
- POLYNOMIALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions
9 Videos
- STATISTICS AND PROBABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS
12 Videos
Similar Questions
Find ∠A+∠B+∠C+∠D
View SolutionABCD is a quadrilateral in which AB=BC and AD=CD ,Show that BD bisects both the ∠ABC and ∠ADC.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
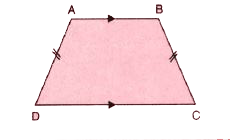
∠C=∠D
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
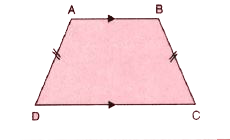
∠A=∠B
View SolutionIn quadrilateral ABCD, AD = BC and BD = CA. Prove that :
(i) ∠ADB=∠BCA
(ii) ∠DAB=∠CBA
View SolutionThe following figure shows a quadrilateral in which sideo AB and DC are parallel. If ∠A:∠D=4:5,∠B=(3x−15)∘and∠C=(4x+20)∘, find each angle of the quadrilateral ABCD.

View SolutionIn a quadrilateral ABCD, AB= AD and CB= CD. Prove that:
AC bisects angle BAD
View SolutionBisectors of angles A and D of a quadrilateral ABCD meet at P. Prove that ∠APD=12(∠B+∠C)
View SolutionABCD is a trapezium in which AB∣∣DCand∠A=∠B=45∘. Find angles C and D of the trapezium.
View SolutionThe figure, given alongside, shows a trapezium ABCD in which AB/DC and AD= BC. Prove that:
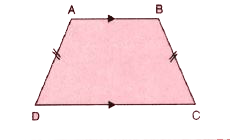
Diagonal AC= diagonal BD
View Solution
