ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR ∣∣ ACand SR=12AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
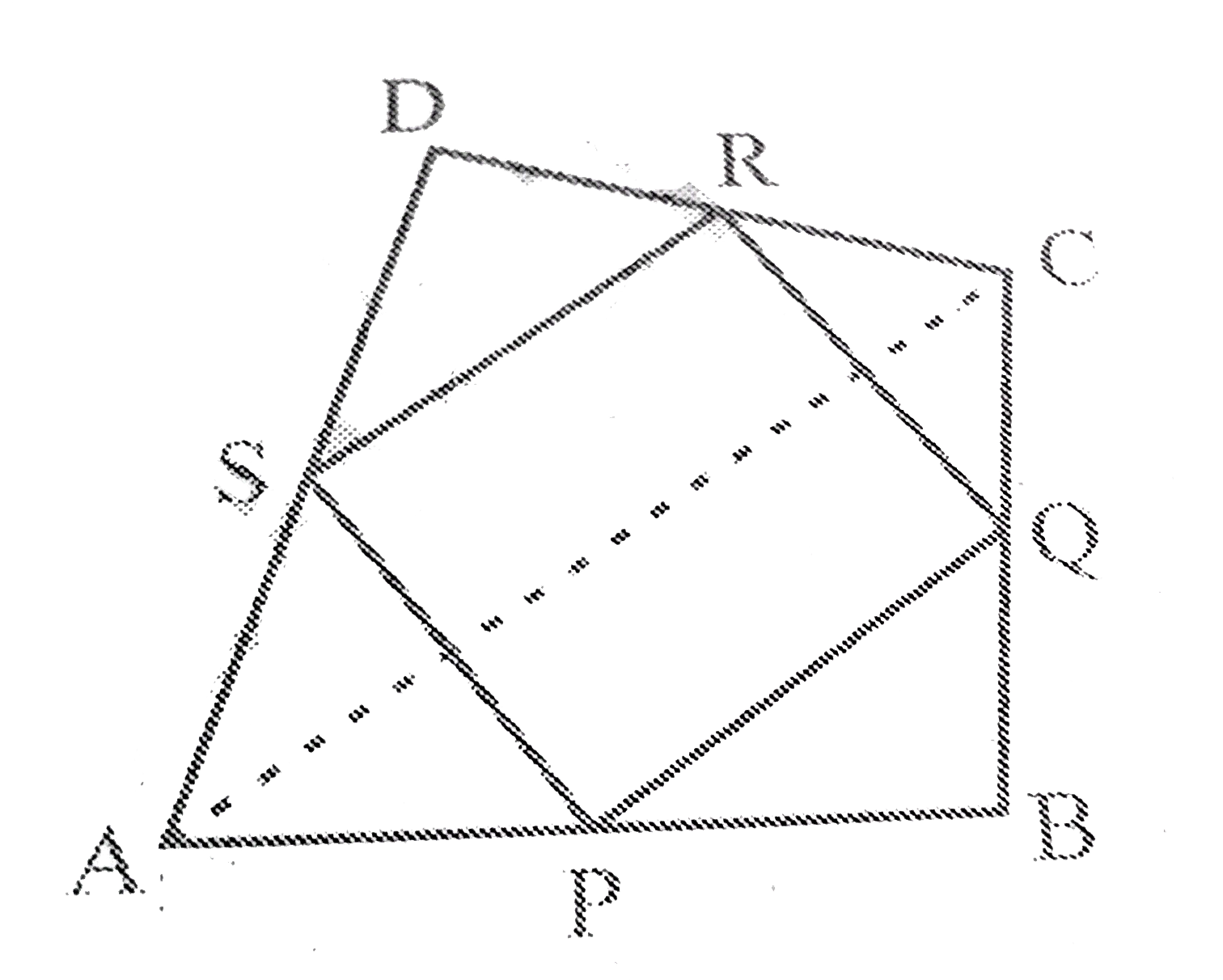
In the triangle, ΔACD, S and R are midpoints of AD and CD.
So, from Midpoint theorem, we can say that,
SR∣∣AC and SR=12AC->(1)
Similarly, in the triangle, ΔACB, P and Q are midpoints of AB and CB.
So, from Midpoint theorem, we can say that,
PQ∣∣AC and PQ=12AC->(2)
From (1) and (2),
SR=PQ=12AC
Also, as both SR and PQ are parallel to AC, so, both of them should also be parallel to each other.
So, PQ=SRandPQ∣∣SR
Similarly, we can show that , SP∣∣RQandSP=RQ
Thus, PQRS is a parallelogram.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NCERTCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 8.1
12 Videos
- QUADRILATERALSBOOK - NCERTCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES
8 Videos
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES
10 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.1
2 Videos
Similar Questions
Prove that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rhombus and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
View SolutionABCD is a quadirlateral in which AD= BC. If P,Q,R,S be the midpoints of AB,AC,CD and BD respectively, show that PQRS is a rhombus.
View SolutionSuppose ABCD is a rectangled and P,Q,R,S are points on the sides AB,BC,CD,DA respectively. Show that PQ+QR+RS+SP>√2AC.
View SolutionABCD is a quadrilateral; P,Q,RandS are the points of trisection of side AB,BC,CDandDA respectively and are adjacent to AandC ; prove that PQRS is parallelogram.
View SolutionABCD is a square. P, Q, R, S are points on the sides AB. BC, CD, DA respectively such that AP = BQ = CR = DS. What is ∠SPQ equal to ?
View SolutionABCD is a parallelogram in which P and Q are mid-points of opposite sides AB and CD (see Fig. 8.18). If AQ intersects DP at S and BQ intersects CP at R, show that: (i) APCQ is a parallelogram.(ii) DPBQ is a parallelogram.(iii) PSQR is a parallelogram
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View SolutionLet ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View Solution
