ABCD is a quadirlateral in which AD= BC. If P,Q,R,S be the midpoints of AB,AC,CD and BD respectively, show that PQRS is a rhombus.
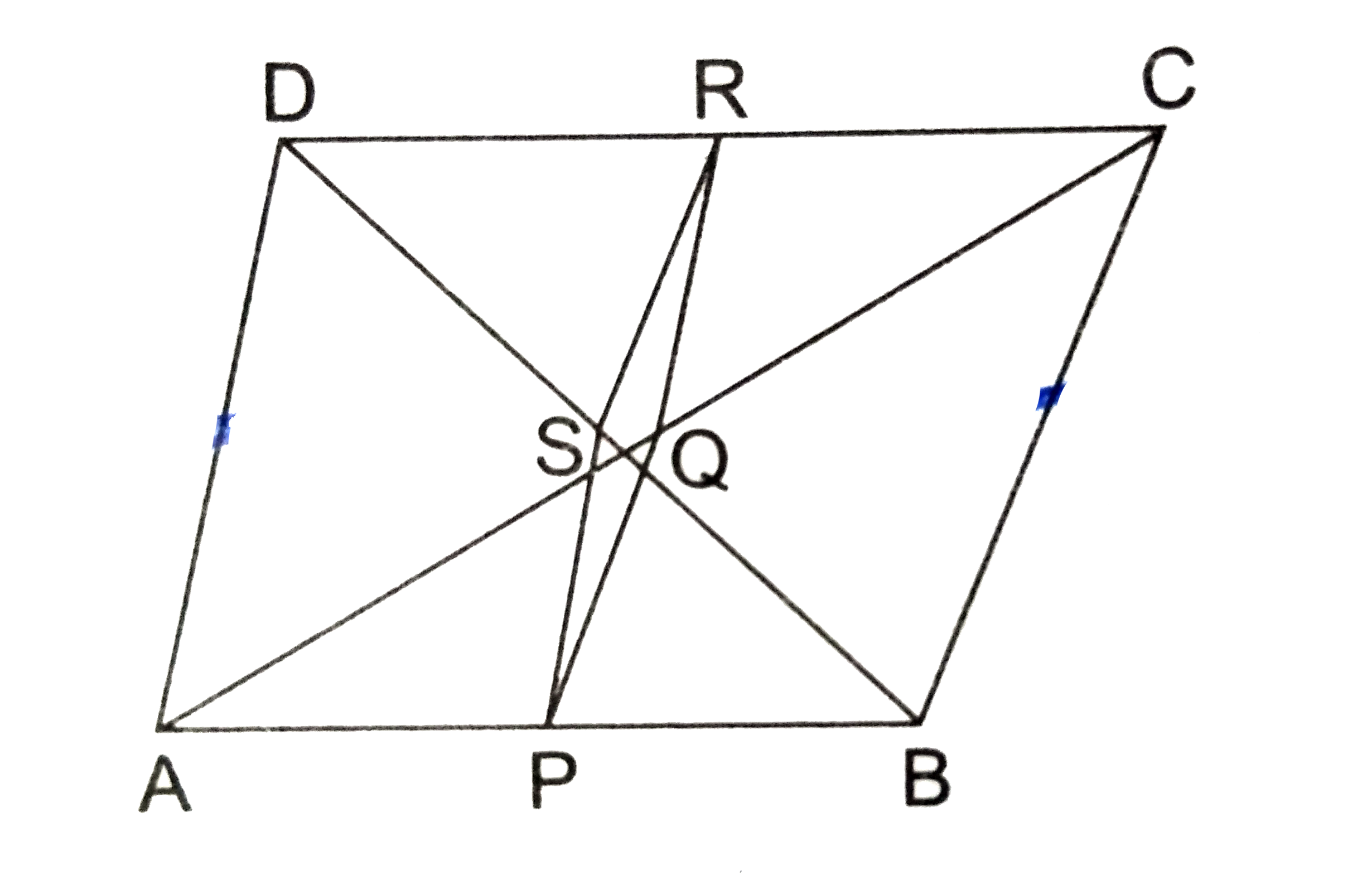
In ΔABC,PandQ are midpoints of AB and AC respectively.
∴PQ∣∣BC [ by midpoint theorem]
And so, ΔAPQ~ΔABC
⇒APAB=AQAC=PQBC⇒PQBC=12⇒PQ=12BC=12DA[∴AP=12ABandBC=DA]
In ΔCDA,PQ∣∣DAandRQ=12DA.
In ΔBDA,SP∣∣DAandSP=12DA.
In ΔCDB,SR∣∣BCandSR=12BC=12DA.
∴SP||RQandPQ||SRandPQ=RQ=SP=SR

Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C
13 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7D
22 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7A
12 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
ABCD is rectangle formed by the points A(-1, -1), B(-1, 4), C(5, 4) and D(5, -1). If P, Q, R and S be the midpoint of AB, BC, CD and DA respectively, show that PQRS is a rhombus.
View SolutionIn the given figure, ABCD is a rectangle in which AB = 40 cm and BC = 25 cm. If P. Q, R, S be the midpoints of AB, BC, CD and DA respectively, find the area of the shaded region.
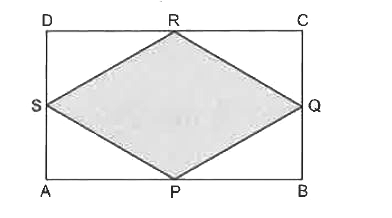
View Solution
Knowledge Check
If ABCD be a rectangle and P, Q, R, S be the mid-points of AB, BC, CD and DA respectively, then the area of the quadrilateral PQRS is equal to
A13 are (ABCD)B34 area (ABCD)C12 area (ABCD)Darea (ABCD)
In the given figure, ABCD is a rectangle in AB−40cmandBC=25cm. If P,Q,R,S be the mid-points of the sides AB,BC,CDandDA respectively, find the area of the shaded region.
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View SolutionABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that :
(i) SR ∣∣ ACand SR=12AC
(ii) PQ = SR
(iii) PQRS is a parallelogram.
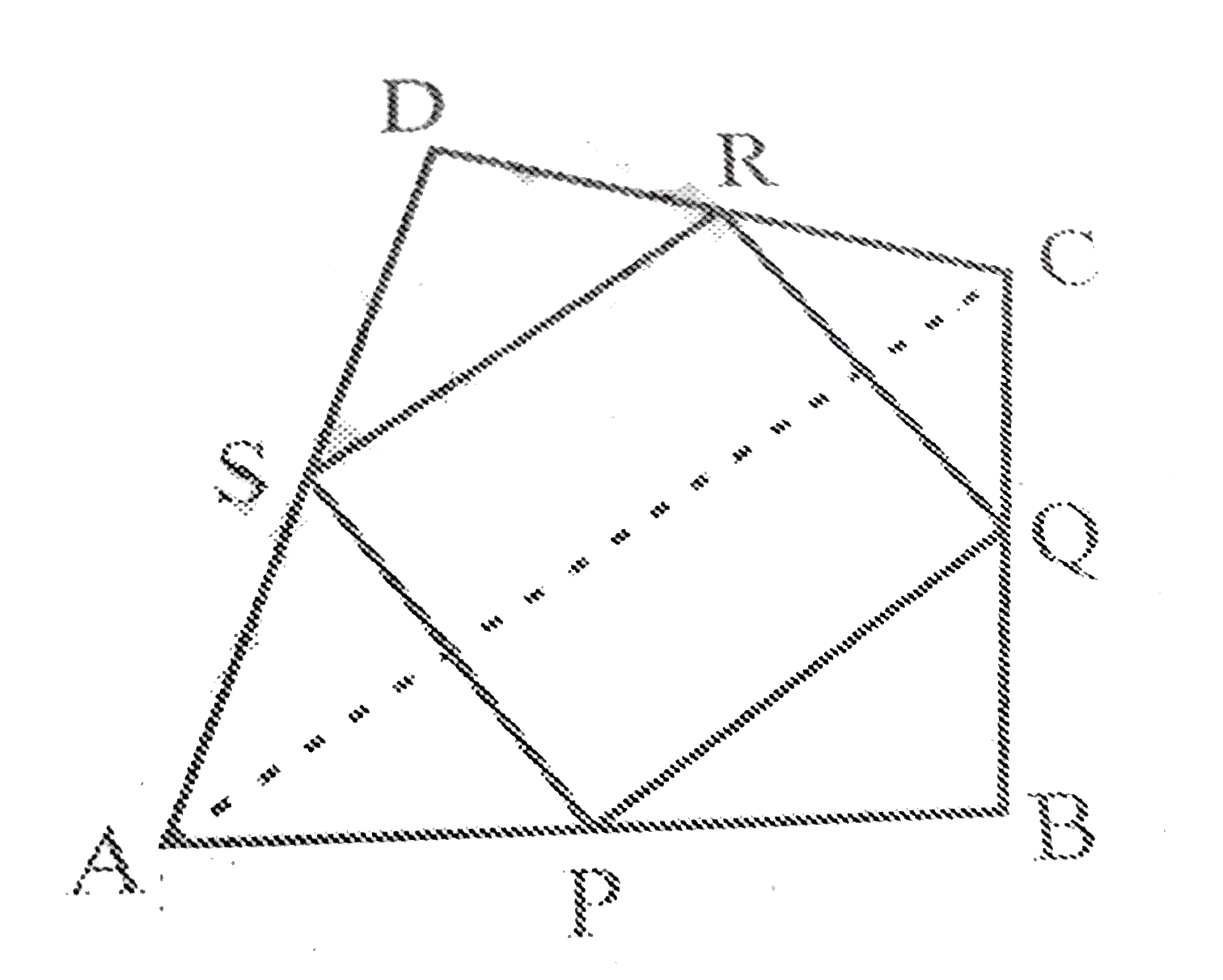
View SolutionABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionLet ABCD be a rectangle. Let P, Q, R, S be the mid-points of sides AB, BC, CD, DA respectively. Then the quadrilateral PQRS is a
View SolutionABCD is a square of area 1 m2. P and Q are the midpoints of AB and BC respectively. What is the area of Δ DPQ ?
View SolutionABCD is a quadrilateral; P,Q,RandS are the points of trisection of side AB,BC,CDandDA respectively and are adjacent to AandC ; prove that PQRS is parallelogram.
View Solution