ABCD is a rectangle and M is a point on CD . AC and BM meet at X .

It is given that CM =3MD. Find
(i) area of ΔCXM : area of ΔAXB
(ii) area of ΔBXC : area of rectangle ABCD
(i) 9:16
(ii) 3:11
(i) 9:16
(ii) 3:14
(i) 16:9
(ii) 14:3
(i) 16:9
(ii) 11:3
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
ABCD is a rectangle and there are four equilateral triangles . Area of ΔASD equals to area of ΔBQC and area of ΔDRC equals to area of ΔAPB. The perimeter of the rectangle is 12 cm. Also the sum of the areas of the four triangles is 10√3cm2 then the total area of the figures thus formed :
 A2(4+5√3)cm2B5(4+2√3)cm2C42√3Dnone of these
A2(4+5√3)cm2B5(4+2√3)cm2C42√3Dnone of these - Question 2 - Select One
In the figure, ABCD is a rectangle, and F and E are points on AB and BC respectively. The area of ΔDFB is 9 and the area of ΔBED is 24. What is the perimeter of the rectangle?
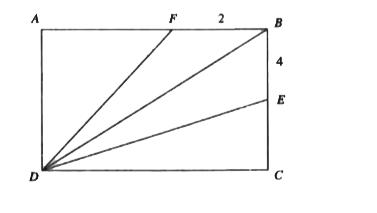 A18B23C30D42
A18B23C30D42 - Question 3 - Select One
In the figure, ABCD is a rectangle, and the area of ΔACE is 10. What is the area of the rectangle?
 A18B22.5C36D44
A18B22.5C36D44
The area of the rectangle ABCD below is 180 cm2.
View SolutionIn a figure, ABCD is a rectangle and P & Q are mid-points of CD and BC respectively. Find ratio of area of shadow region and area of un-shad-owed region?
 View Solution
View SolutionLet ABCD be a rectangle and let E and F be points on CD and BC respectively such that area (ADE)=16, area (CEF)=9 and area (ABF)=25 What si the area of triangle AEF?
View SolutionIn the given figure, ABCD is a rectangle; EandF are the mid-points of the sides BCandCD respectively. What is the ratio of the area of ΔAEF and that of ΔECF?
View SolutionIn parallelogram ABCD, E is a point in AB and DE meets diagonal AC at point F. If DF:FE= 5:3 and area of ΔADF is 60cm2, find :
(i) area of ΔADE
(ii) if AE:EB= 4:5, find the area of ΔADB
(iii) also, find area of parallelogram ABCD.View Solution


