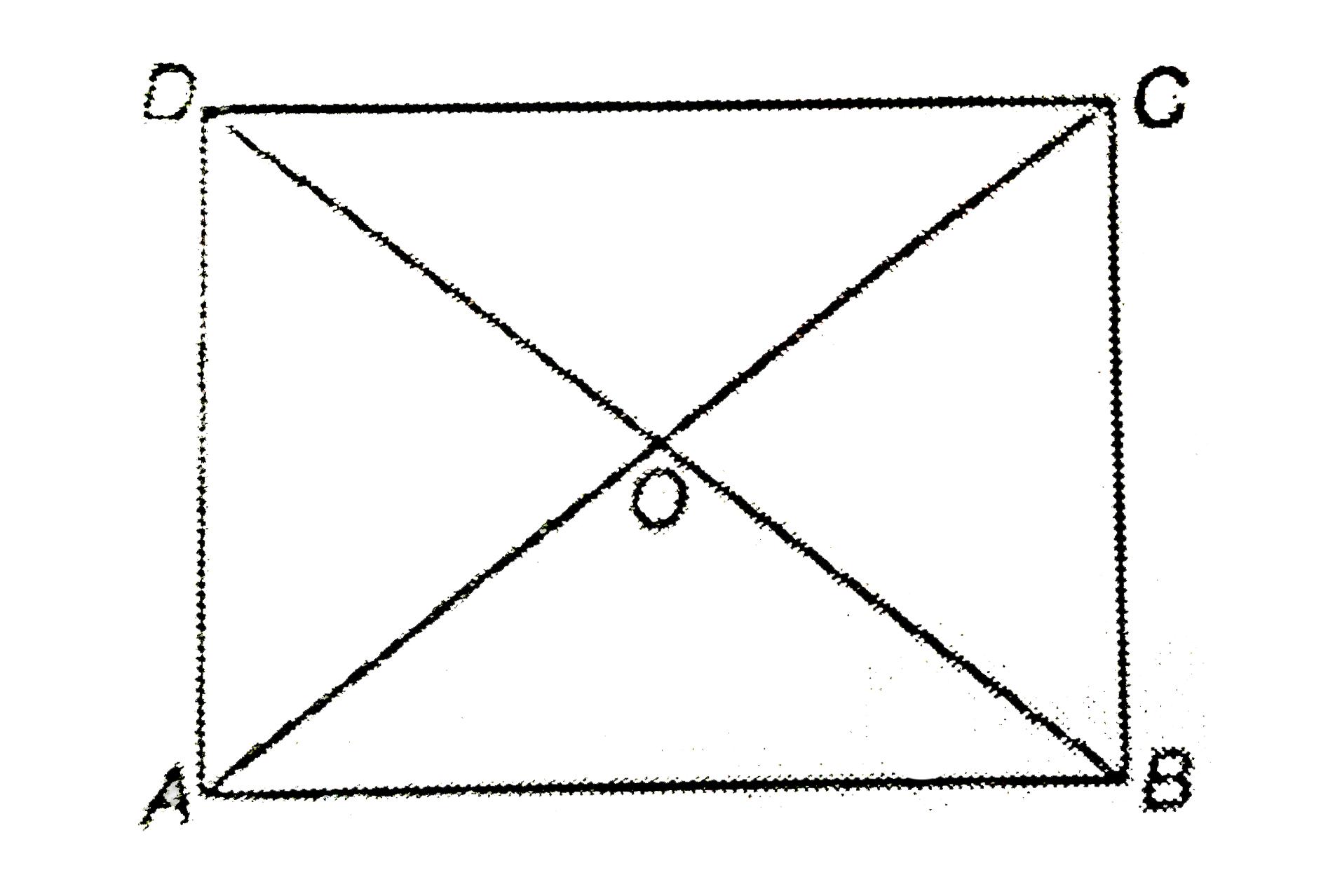
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that: (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D. .
(i) As ABCD is a rectangle and AC bisects ∠A and ∠C,
∴∠DAC=∠BACand∠ACD=∠ACB
As opposite sides of the equal angles are equal,
∴CD=BCandAD=AB
As ABCD is a rectangle,
∴AB=CD=BC=AD
So, ABCD is a square.
(ii) In ΔABDandΔCBD,
AB=CB
AD=CD
∠A=∠C=90∘
So, from RHS congruency, these two triangles are congruent.
∴∠ABD=∠CBD
So, BD bisects ∠B.
Similarly, we can prove BD bisects ∠D.
Similar Questions
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B
 View Solution
View SolutionABCD is a rectangle in which diagonal BD bisects ∠B. Show that ABCD is a square.
View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠Bas well as ∠D.
View SolutionContruct a square ABCD is which
diagonals AC = 9 cmView SolutionABC is an isosceles triangle in which AB=AC. AD bisects exterior angle PAC and CD∣∣AB. Show that(i) ∠DAC=∠BCA and (ii) ABCD is a parallelogram.
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
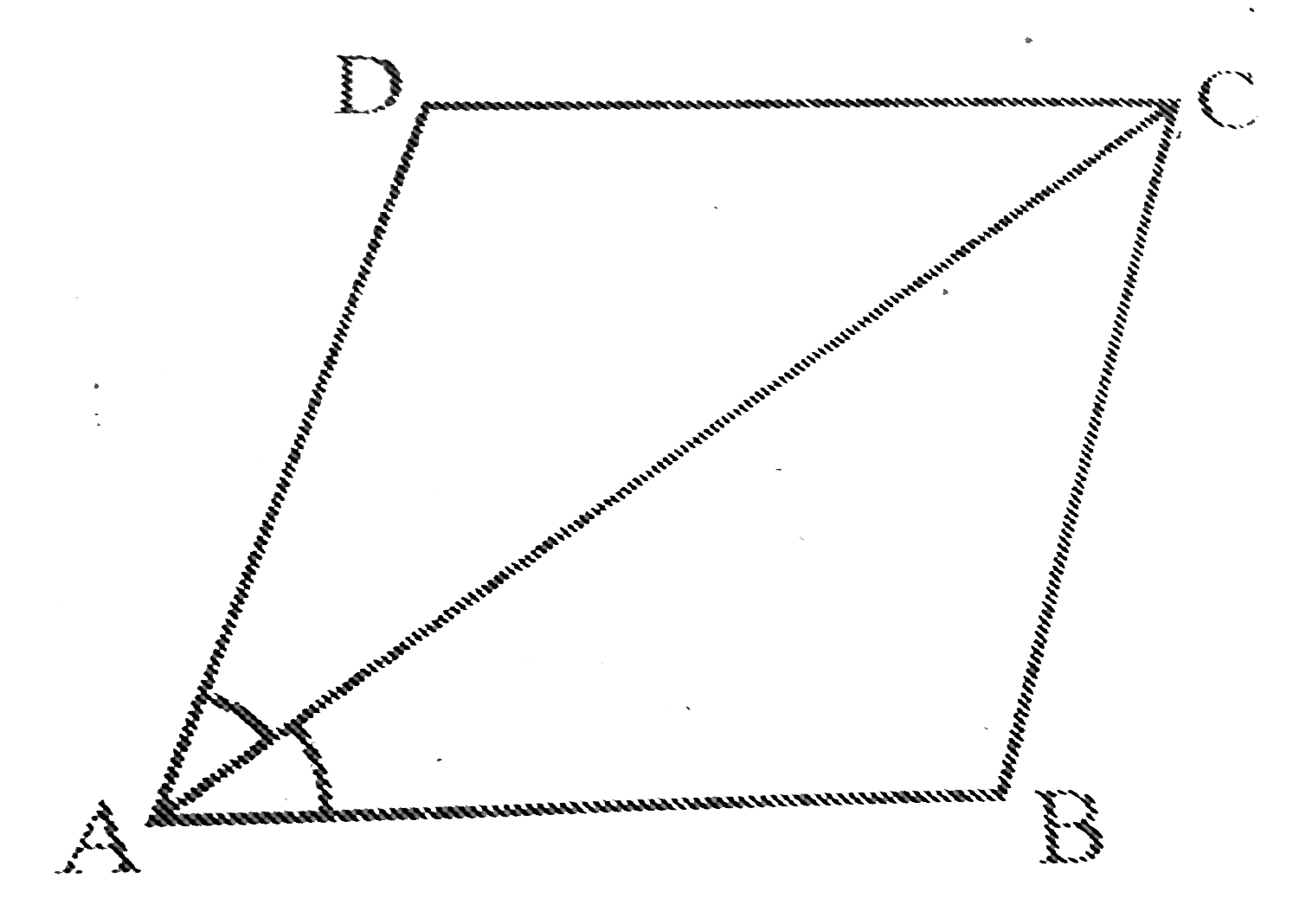
View SolutionDiagonal AC of a parallelogram ABCD bisects ∠A. Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
 View Solution
View SolutionABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC=350 , then ∠ABC= (a) 700 (b) 1100 (c) 900 (d) 1200
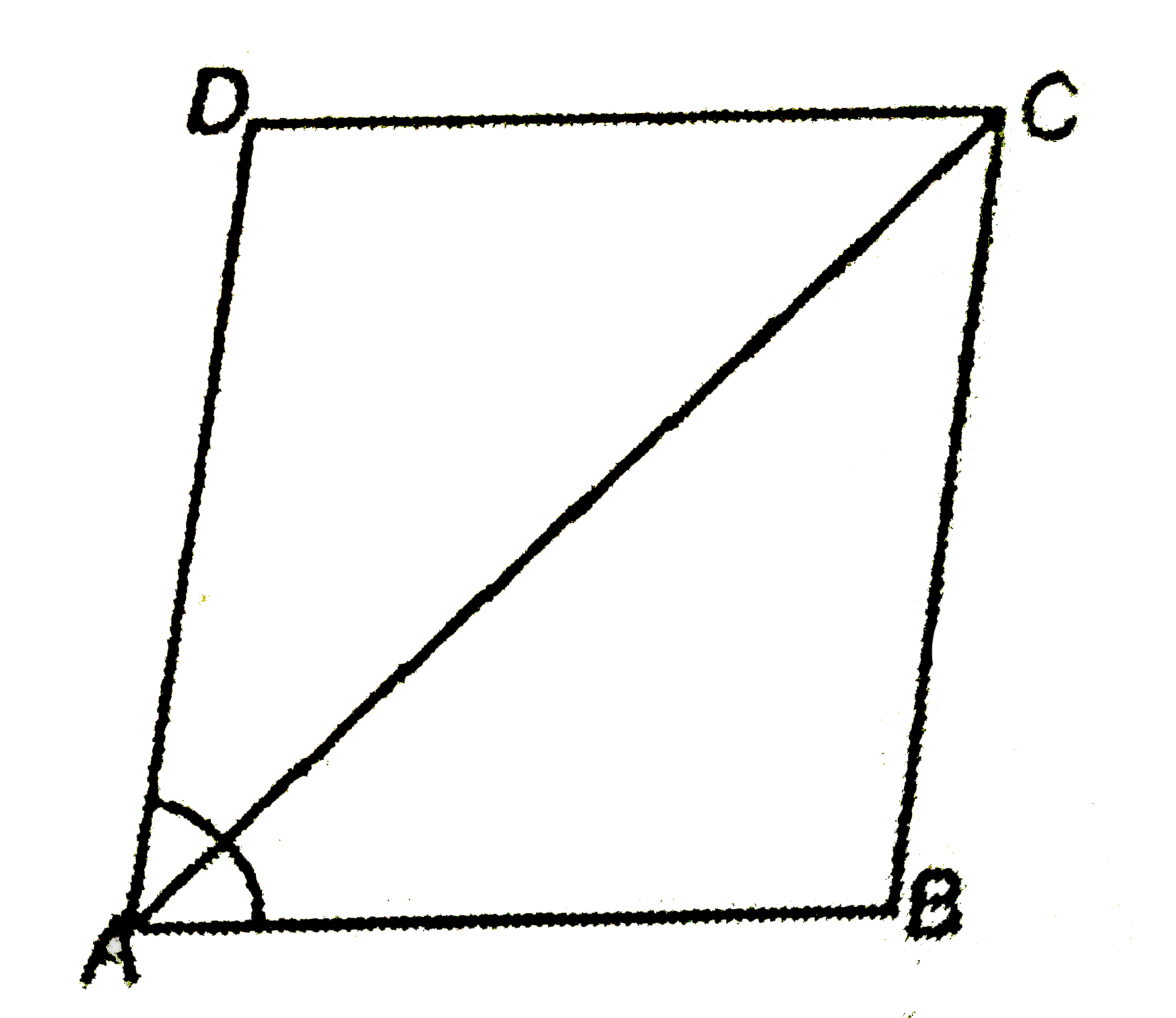
View SolutionDiagonal AC of a paraleligram ABCD bisects ∠A (sec figure). Show that:
(i) it bisects ∠C also (ii) ABCD is a rhombus.
 View Solution
View SolutionShow that the diagonals of a square are equal and bisect each other at right angles.
View Solution

