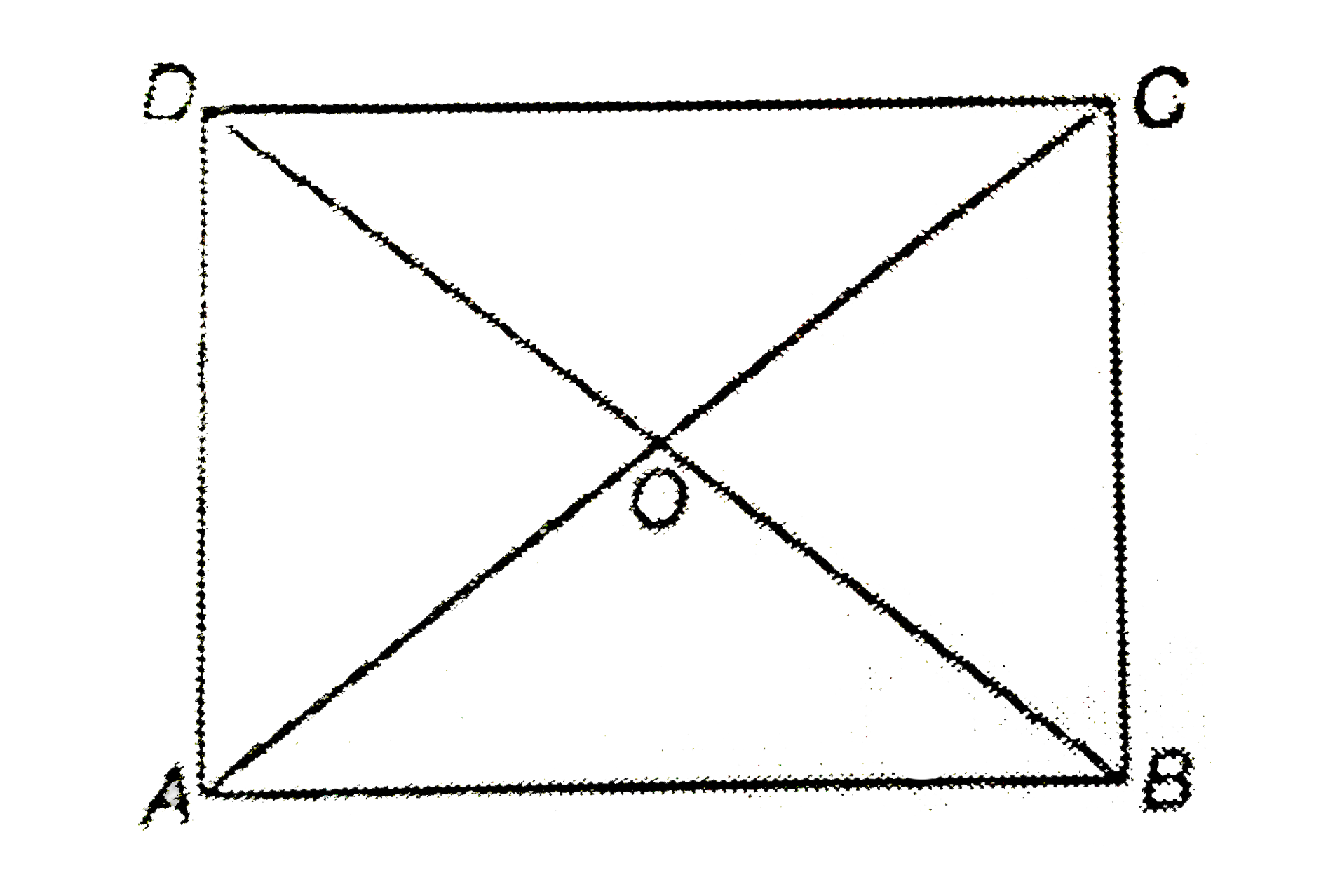
ABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:
(i) ABCD is a square
(ii) diagonal BD bisects ∠Bas well as ∠D..
Video Solution
Text Solution
(i) As ABCD is a rectangle and AC bisects ∠A and ∠C,
∴∠DAC=∠BACand∠ACD=∠ACB
As opposite sides of the equal angles are equal,
∴CD=BCandAD=AB
As ABCD is a rectangle,
∴AB=CD=BC=AD
So, ABCD is a square.
(ii) In ΔABDandΔCBD,
AB=CB
AD=CD
∠A=∠C=90∘
So, from RHS congruency, these two triangles are congruent.
∴∠ABD=∠CBD
So, BD bisects ∠B.
Similarly, we can prove BD bisects ∠D.
|
Similar Questions
Knowledge Check
If in a rectangle ABCD, diagonal AC bisect ∠A as well as ∠C then ABCD is a
AParallelogramBsquareCRhombusDTrapeziumThree statements are given below:
I. In a rectangle ABCD, the diagonal AC bisects ∠A as well as ∠C.
II. In a square ABCD, the diagonal AC bisects ∠A as well as ∠C.
III. In a rhombus ABCD, the diagonal AC bisects ∠A as well as ∠C.
Which is true?AI onlyBII and IIICI and IIIDI and IIABCD is a quadrlateral in which BD and AC are diagonals then
AAB+BC+CD+AD<AC+BDBAB+BC+CD+DA>AC+BDCAB+BC+CD+DA=AC+BDDAB+BC+CD+DA>2(AC+BD)
ABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠B as well as ∠D.
View SolutionIf ABCD is a quadrilateral whose diagonals AC and BD intersect at O, then

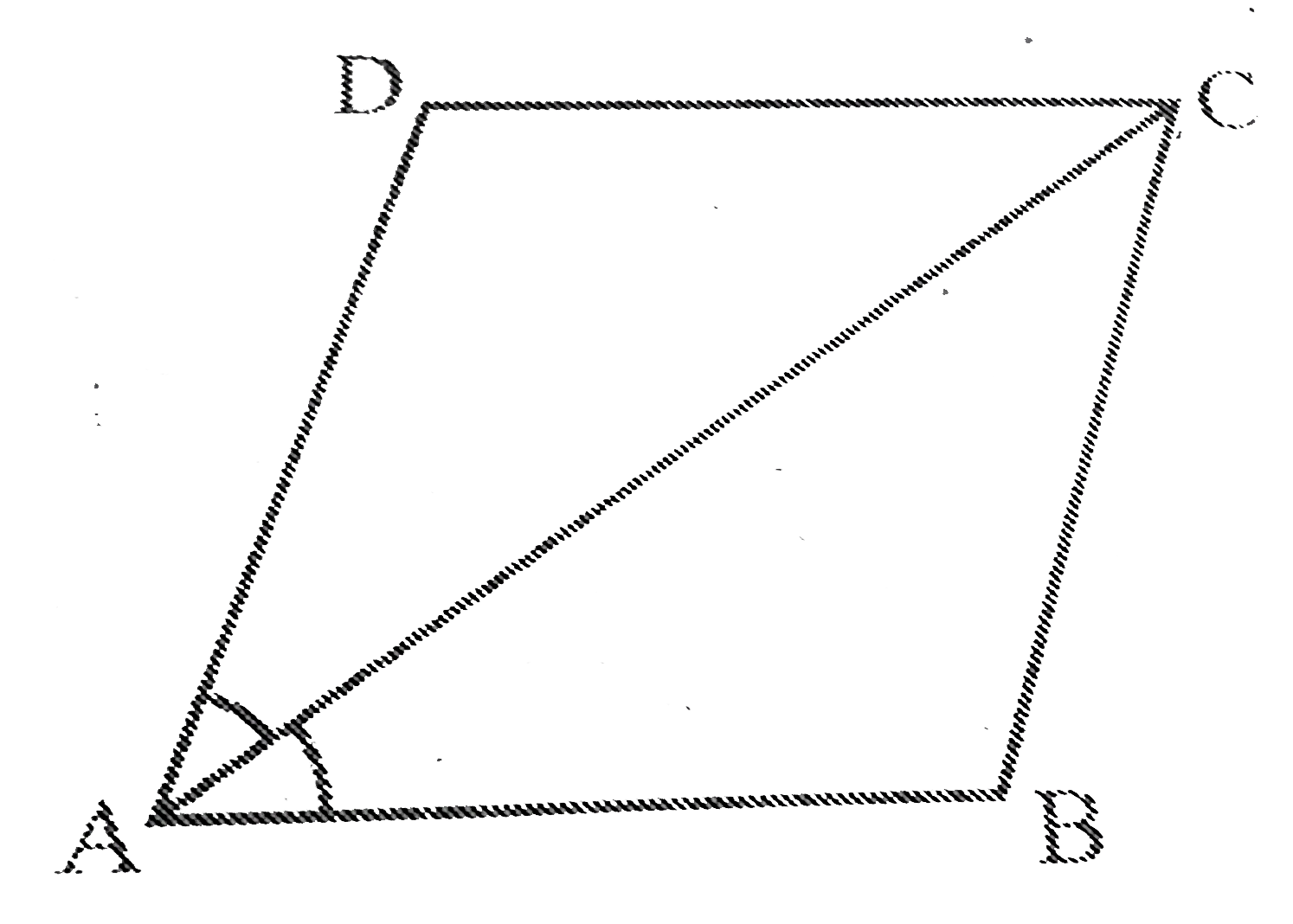
View SolutionDiagonal AC of a parallelogram ABCD bisects ∠A. Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
View SolutionABCD is a rectangle. The diagonals AC and BD intersect at O. If AB = 32 cm and AD = 24 cm, then what is OD equal to ?
View SolutionIn figure, ABCD is a rectangle in which diagonal D AC is produced to E. If ∠ECD=146∘, find ∠AOB.

View Solution