ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B
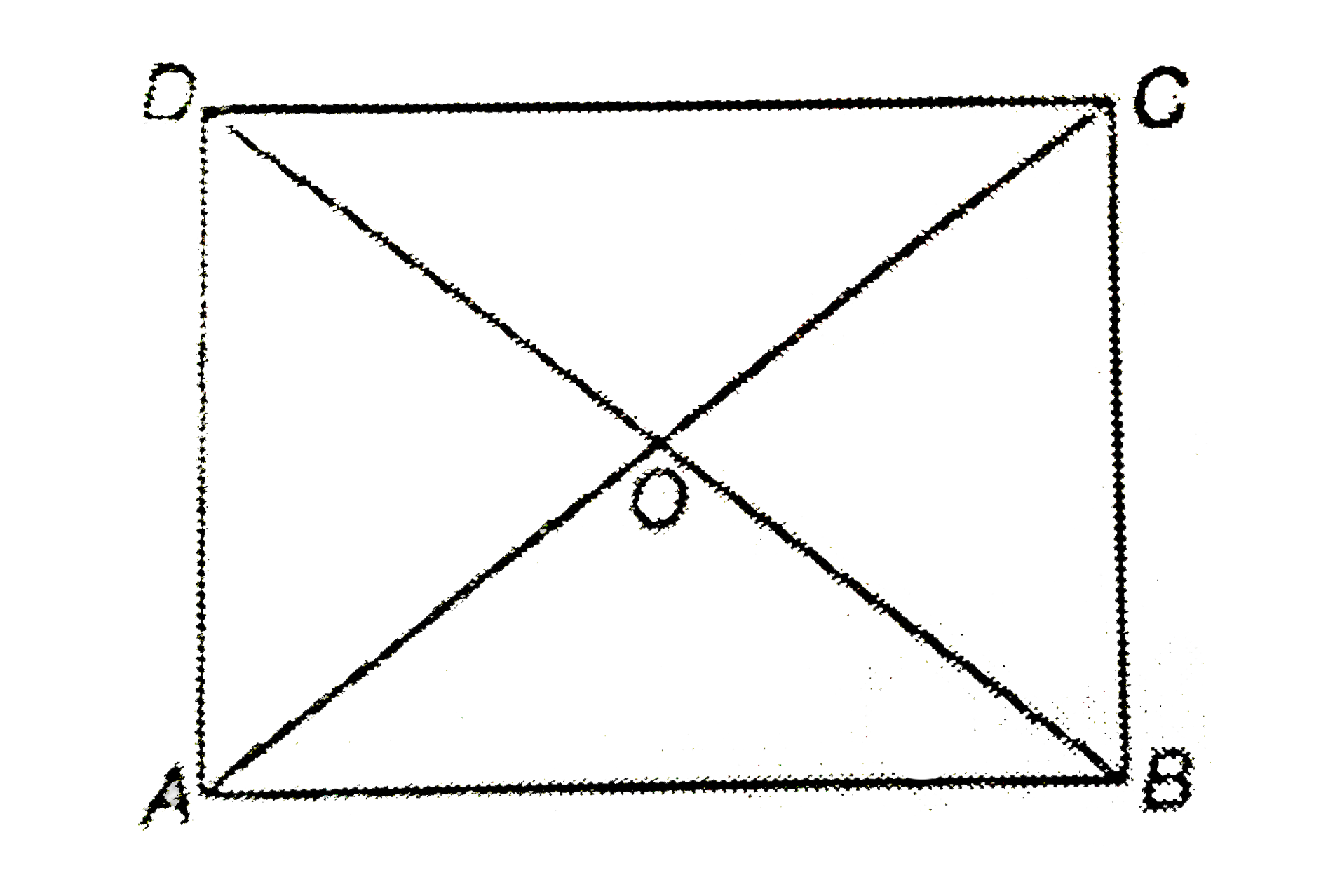
ABCD is a reactangle.
∴ AB=CDandBC=AD ...(1)
To prove : (1) ABCD is a square.
i.e., AB=BC=CD=DA
(ii) Diagonal AD bisects ∠B as well as ∠D.
Proof : (i) In ΔABCDandΔABC, transversal interects
∵⎧⎪⎨⎪⎩∠DAC=∠BAC(given)∠DCA=∠BCA(given)AC=CA(common)
∴ ΔADC≅ΔABC (by ASA rule)
∴ AD=AB (c.p.c.t.)
and CD=BC ...(2)
Hence, from eqs. (1) and (2), we get
AB=BC=AD=CD
∴ ABCD is a square.
(ii) In ΔAOBandΔCOB
∵⎧⎪⎨⎪⎩AB=BC(side of square)BO=OB(common)OA=OC(∵diagonals of square bisect each other)
∴ ΔAOB≅ΔCOB (by SSS rule)
∴ ∠OBA=∠OBC (c.p.c.t)
This shows that BO or BD bisect ∠B.
Similarly, in ΔAODandΔCOD
∵⎧⎪⎨⎪⎩AD=CD(side of square)OD=DO(common)OA=OC(∵diagonals of square bisect each other)
∴ ΔAOD≅ΔCOD (by SSS rule)
∴ ∠ADO=∠CDO
This shows that DO or DB bisect ∠D.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
ABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:(i) ABCD is a square (ii) diagonal BD bisects ∠Bas well as ∠D..
View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that: (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D. .
View SolutionABCD is a rectangle in which diagonal BD bisects ∠B. Show that ABCD is a square.
View SolutionABCD is a parallelogram and AE and CF bisect ∠Aand∠C respectively. Prove that AE||FC.

View SolutionABCD is a rhombus. Show that diagonal AC bisects ∠Aas well as ∠Cand diagonal BD bisects ∠Bas well as ∠D.
View SolutionThe diagonals of a rectangle bisect each other
View SolutionIn the given figure, ABCD is a rectangle, whose diagonals intersect at 'O'. Diagonal AC is produced to E and ∠DCE=145∘.
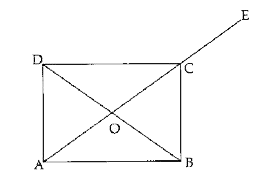
Find : (i) ∠CAB (ii) ∠AOB
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
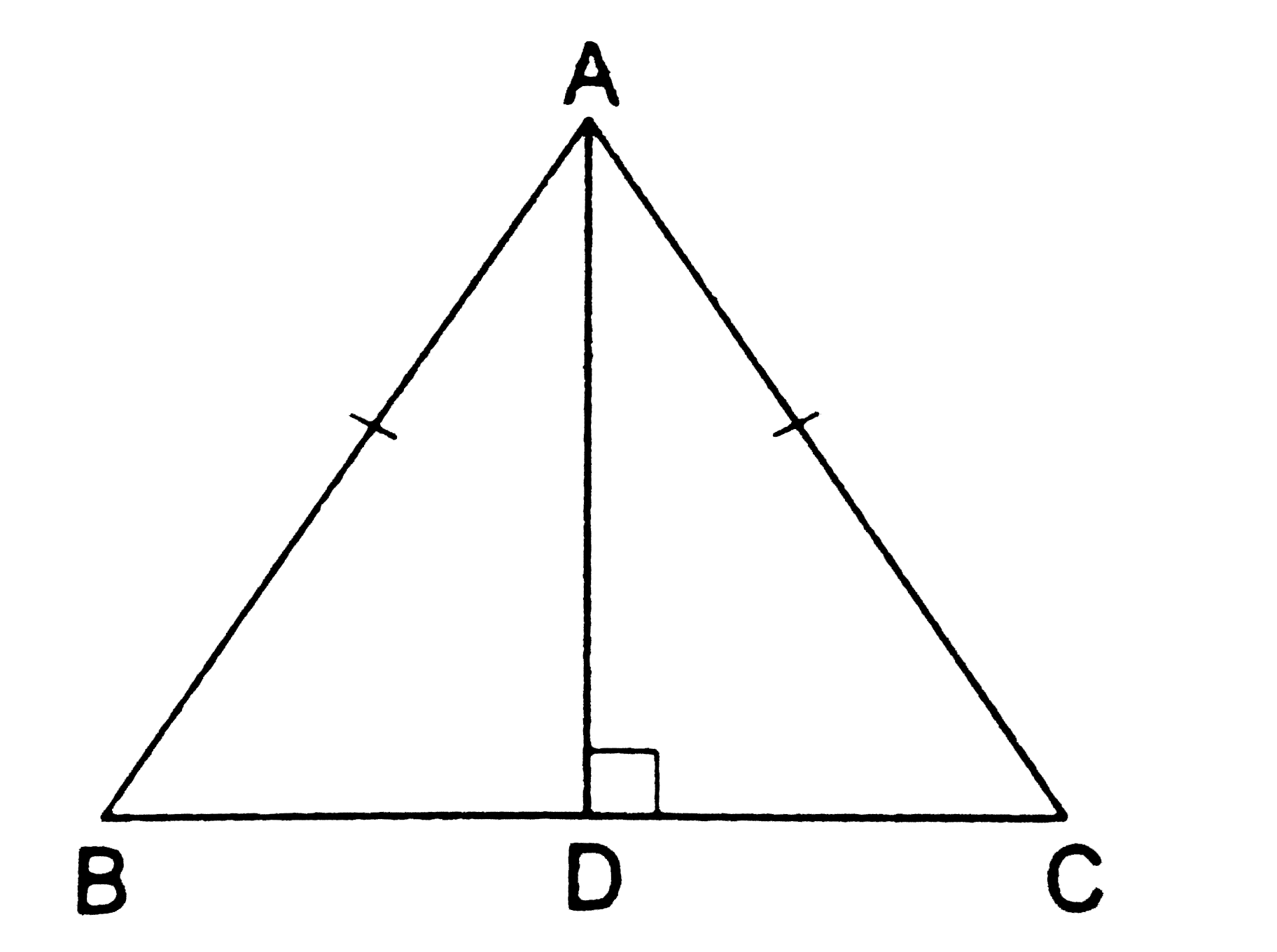
View SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
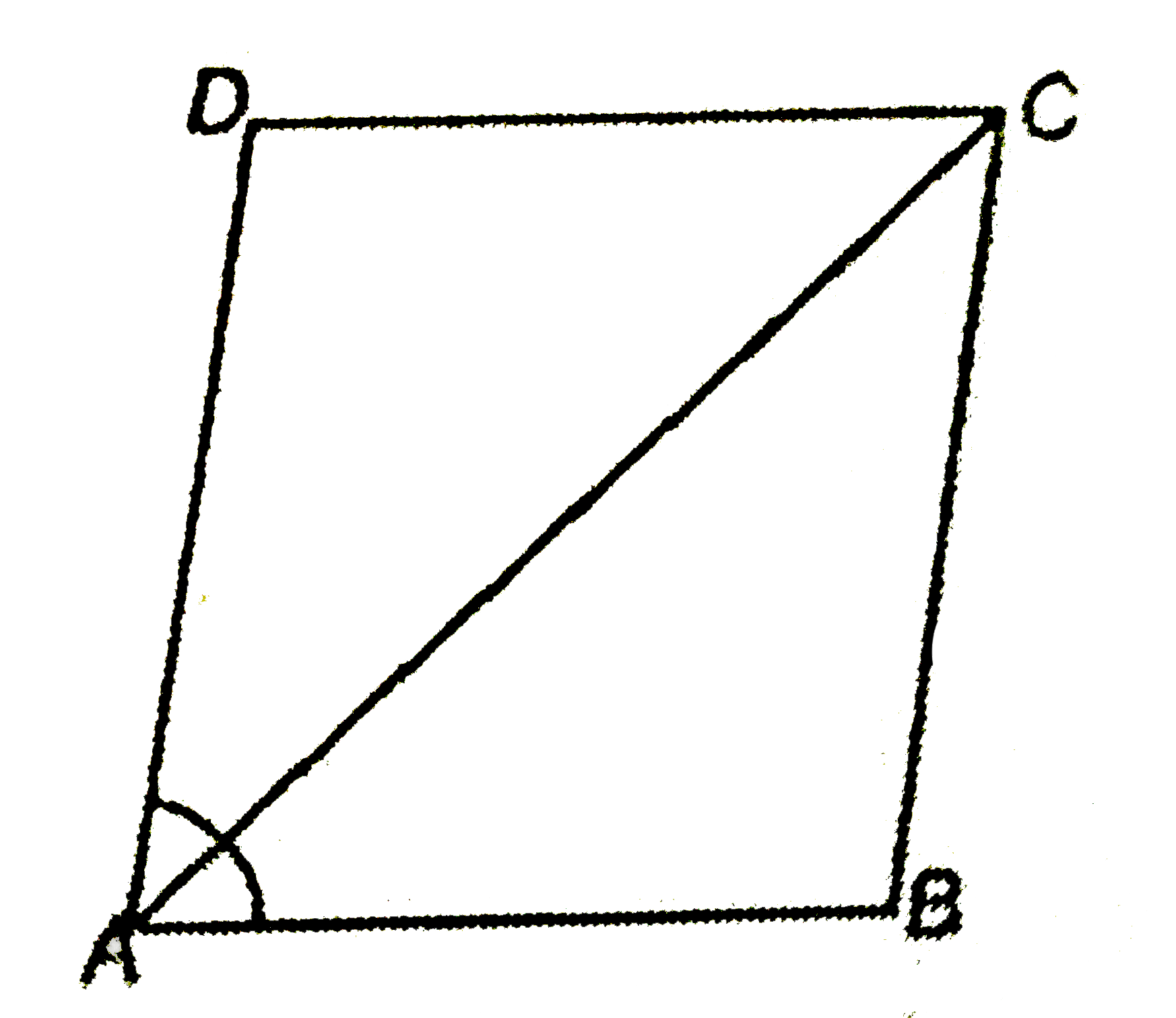
View SolutionDiagonal AC of a paraleligram ABCD bisects ∠A (sec figure). Show that:
(i) it bisects ∠C also (ii) ABCD is a rhombus.
View Solution
