Prove that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
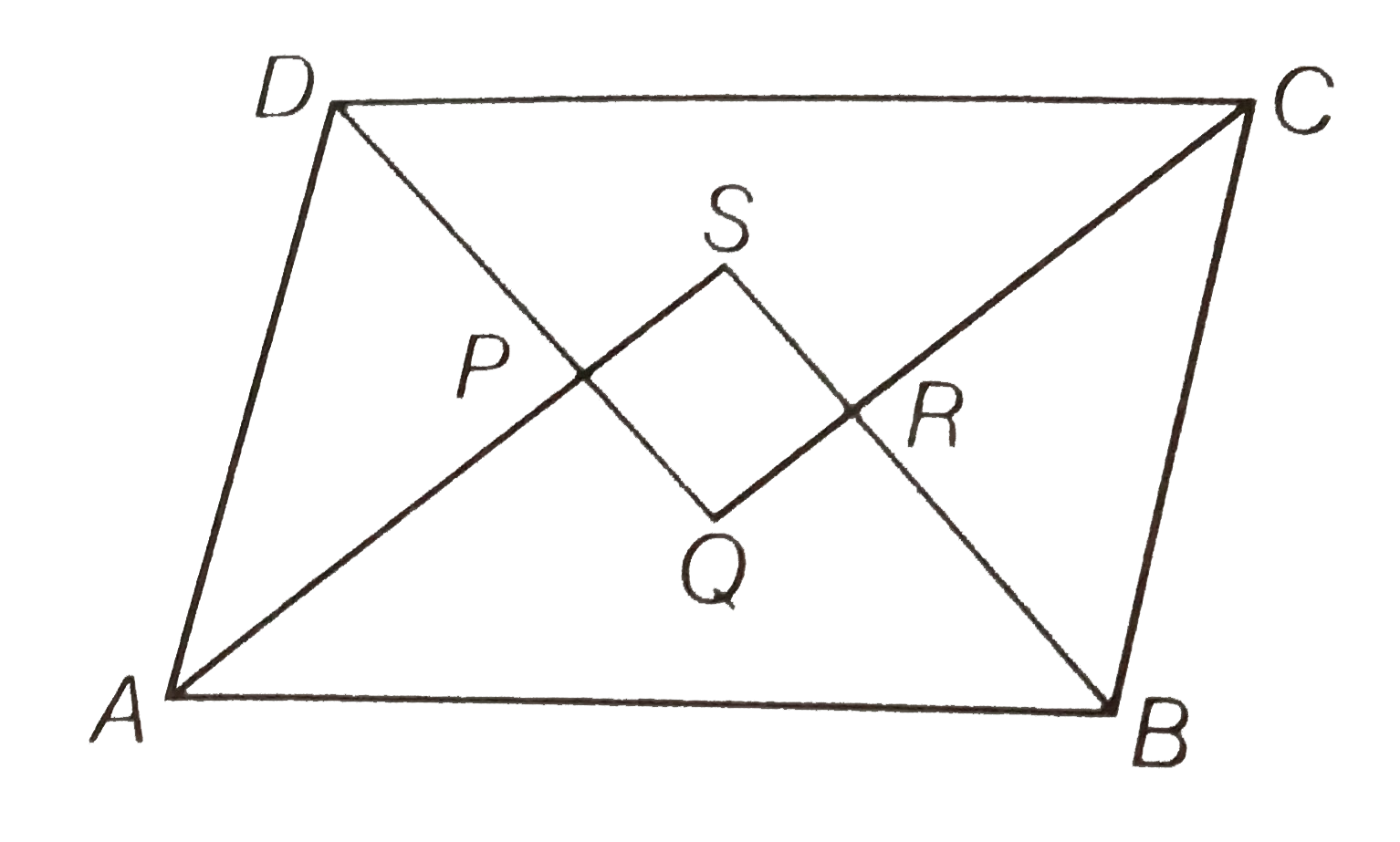
Given : A parallelogram ABCD in which bisectors of angles A,B, C,D intersect at P,Q,S to from a quadrilaateral PQRS.
To prove : PQRS is a rectangle.
Proof: Since, ABCD is a parallelogram.
Therefore, AB||DC
Now, AB||DC and transversal AD interects them at D and A respectively.
Therefore,
∠A+∠D=180∘ (∵sum of consective interior angles is180∘)
⇒ 12∠A+12∠D=90∘
⇒ ∠DAS+∠ADS=90∘ ...(1)
(∵DS and AS are bisectors of∠Aand∠Drespectively)
But , in ΔDAS we have
∠DAS+∠ASD+∠ADS=180∘ (∵sum of angle of a triangle is180∘)
⇒ ∠90∘+∠ASD=180∘ [using(1)]
⇒ ∠ASD=90∘
⇒ ∠PSR=90∘ (∵∠SADand∠PSRare vertically opposite angle∴∠PSR=∠ASD)
Similarly, we can prove that
∠SEQ=90∘,∠RQP=90∘and∠SPQ=90∘
Hence, PQRS is a rectangle.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (long Answer Questions)
5 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
Show that the bisectors of angles of a parallelogram form a rectangle.
View SolutionShow that the bisectors of angles of a parallelogram form a rectangle.
View SolutionTwo parallel lines l and m are intersected by a transversal p . Show that the quadrilateral formed by the bisectors of interior angles is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionProve that any cyclic parallelogram is a rectangle.
View SolutionThe angle bisectors of a parallelogram form a rectangle.
View SolutionProve that the bisectors of opposite angles of a parallelogram are parallel.
View Solution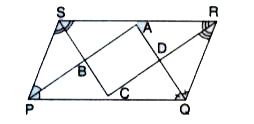
In the alongside diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
Show that:
(i) ∠PSB+∠SPB=90∘
(ii) ∠PBS=90∘
(iii) ∠ABC=90∘
(iv) ∠ADC=90∘
(v) ∠A=90∘
(vi) ABCD is a rectangle
thus, the bisectors of the angles of a parallelogram enclose a rectangle.
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View Solution
