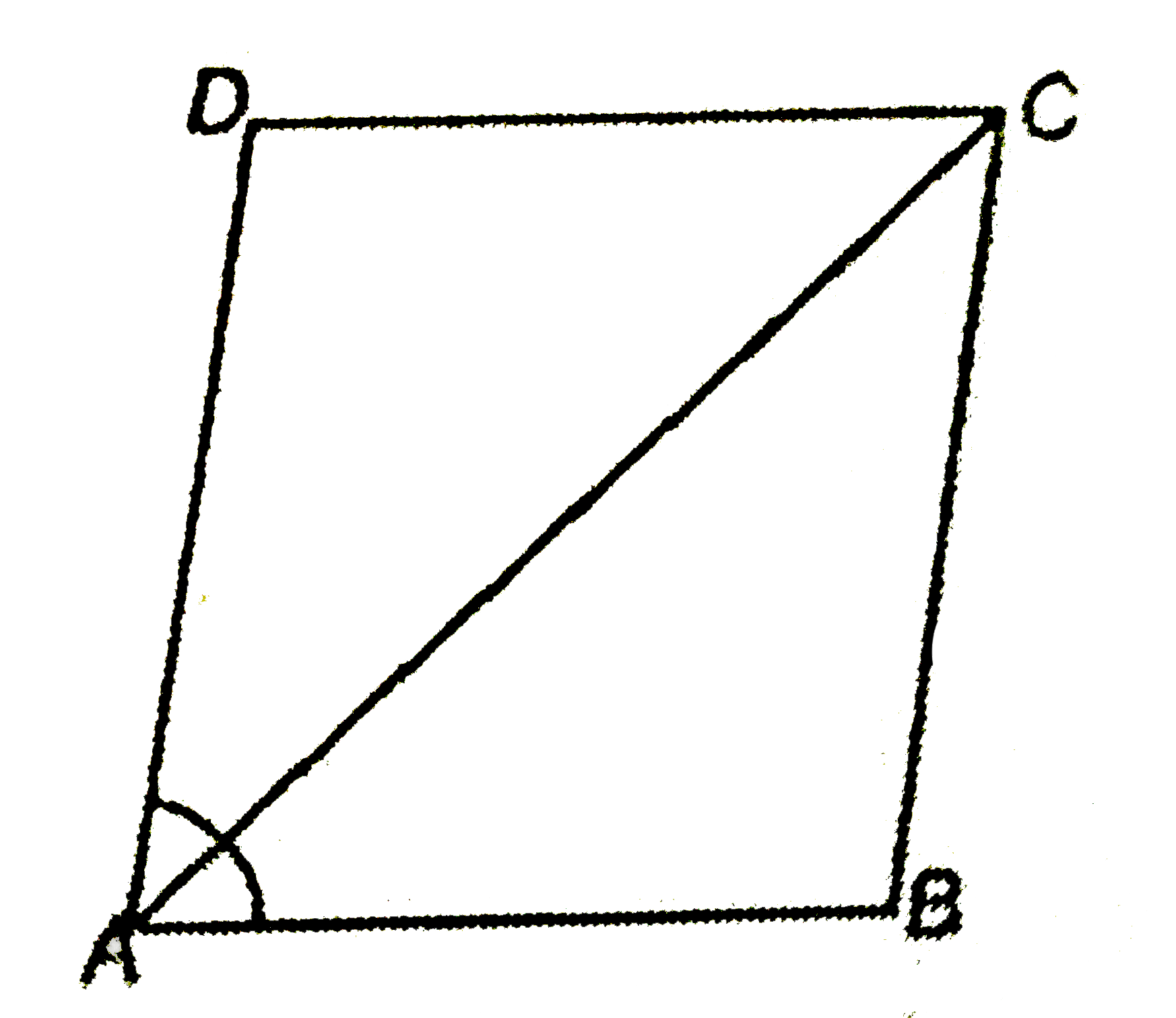
ABCD is a rectangle in which diagonal BD bisects . Show that ABCD is a square.
Given In a rectangle ABCD, diagonal BD bisects .
Construct Join AC.
To show ABCD is a square.
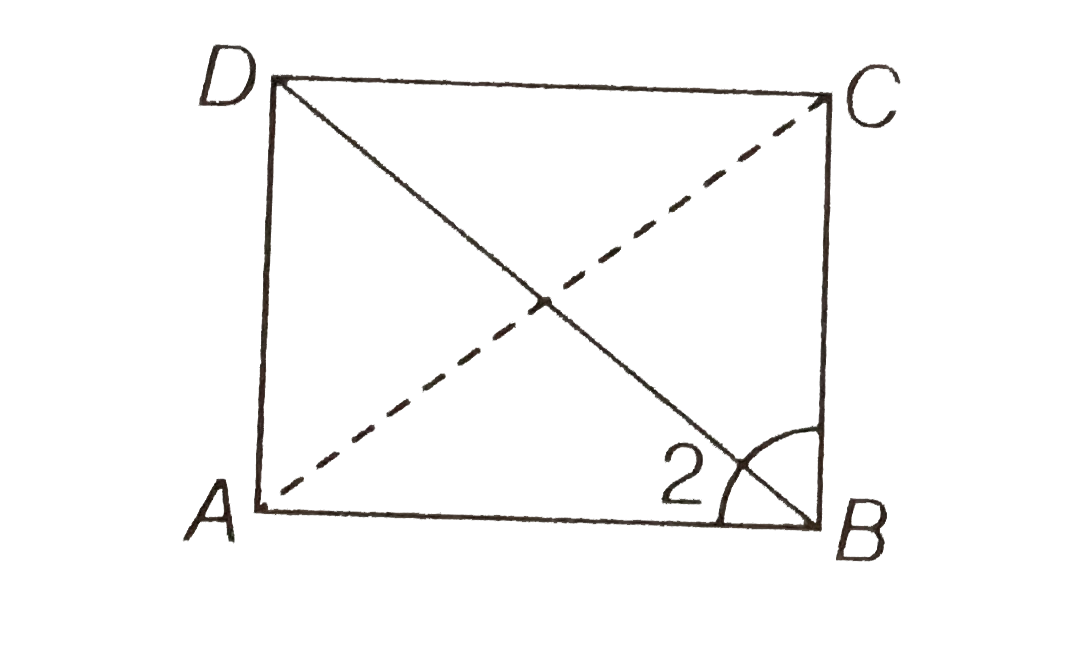
Proof
In BAD and BCD,
and BD=BD [common side]
[by AAS congruence rule]
and [by CPCT rule]...(i)
But in rectangle ABCD, opposite sides are equal.
and
From Eqs. (i) and (ii),
So, ABCD is a square. Hence proved.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS10videos
QUADRILATERALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions9videos
POLYNOMIALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
Similar Questions
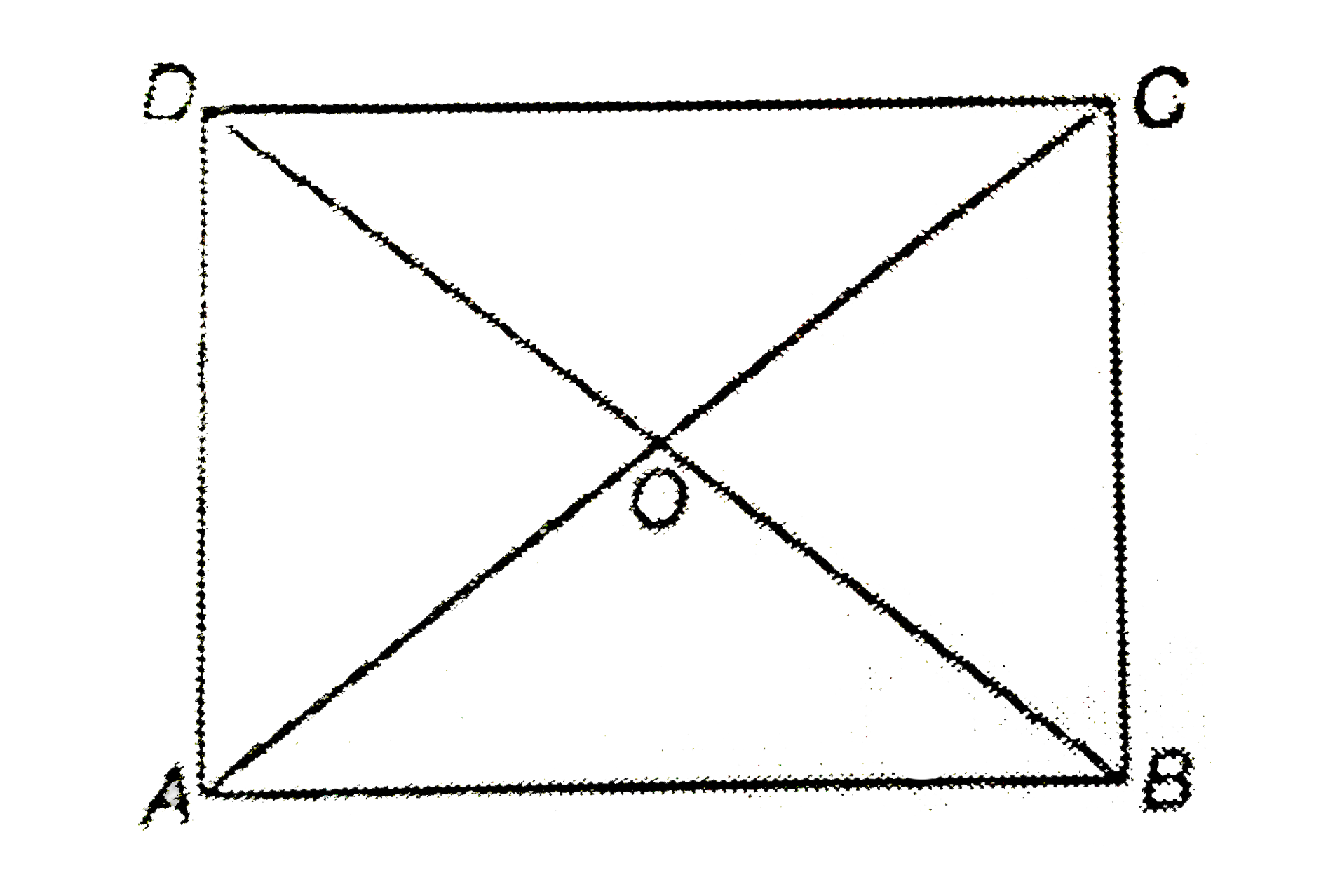
ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B
 View Solution
View SolutionABCD is a rectangle in which diagonal AC bisects ∠Aas well as ∠C. Show that:(i) ABCD is a square (ii) diagonal BD bisects ∠Bas well as ∠D..
View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C . Show that: (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D. .
View SolutionABCD is a parallelogram E is mid-point of AB and DE bisects angle D. Prove that
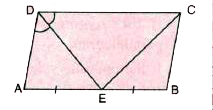
CE bisects angle CView SolutionIn the given figure, ABCD is a rectangle, whose diagonals intersect at 'O'. Diagonal AC is produced to E and ∠DCE=145∘.
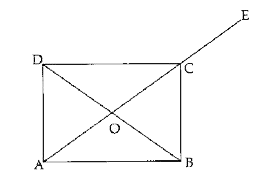
Find : (i) ∠CAB (ii) ∠AOBView SolutionIn a parallelogram ABCD, X and Y are points on diagonal BD such that DX=BY. Prove that AXCY is a parallelogram.
View SolutionThe diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
View SolutionIn a cyclic quadrilateral ABCD the diagonal AC bisects the angle BCD. Prove that the diagonal BD is parallel to the tangent to the circle at point A.
View SolutionDiagonal AC of a paraleligram ABCD bisects ∠A (sec figure). Show that:
(i) it bisects ∠C also (ii) ABCD is a rhombus.
 View Solution
View SolutionThe diagonals of a rectangle intersect each other at right angles. Prove that the rectangle is a square.
View Solution

