ABCD is a rhombus and P, Q, R and S are wthe mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Given In quadrilateral ABCD, P, Q, R and S are the mid-points of the sides AB, BC, CD and DA, respectively.
Also, AC⊥BD
To prove PQRS is a rectangle.
Proof Since, AC⊥BD
∴ ∠COD=∠AOD=∠AOB=∠COB=90∘ ltBrgt In ΔADC, S and R are the mid-points of AD and DC respectively, then by mid-point theorem
SR∣∣ACandSR=12AC ...(i)
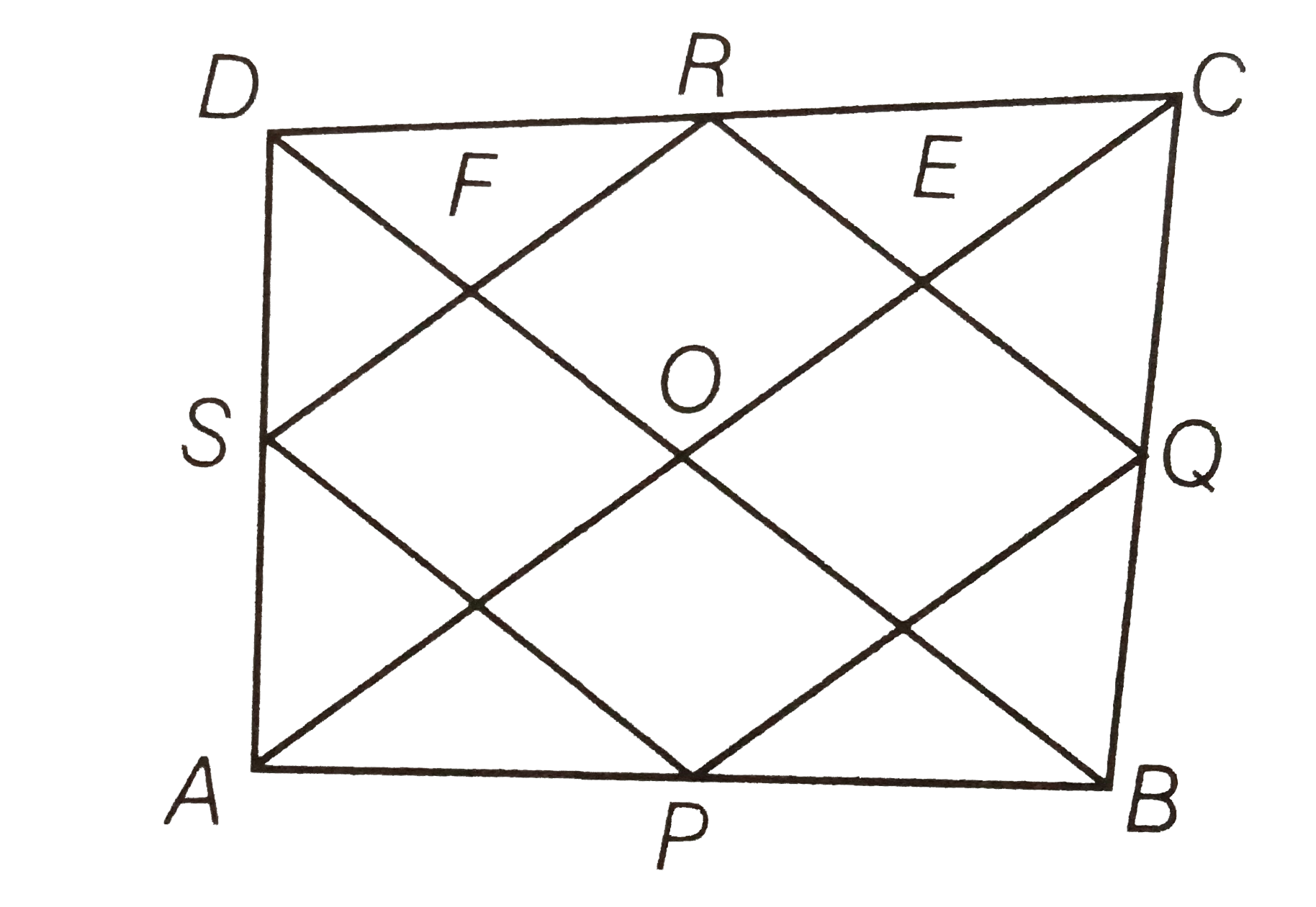
In ΔABC, P and Q are the mid-points of AB and BC respectively, then by mid-point theorem
PQ∣∣ACandPQ=12AC ...(ii)
From Eqs. (i) and (ii), PQ∣∣SRandPQ=SR=12AC ...(iii)
Similarly, SP∣∣RQandSP=RQ=12BD ...(iv)
Now, in quadrilateral EOFR, OE||FR,OF||ER
∴ ∠EOF=∠ERF=90∘ [∵∠COD=90∘⇒∠EOF=90∘]...(v)
So, PQRS is a rectangle. Hence proved.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - QUADRILATERALS EXERCISE - SHORT ANSWER TYPE QUESTIONS10videos
QUADRILATERALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - POLYNOMIALSEXERCISE - EXERCISE 2.4 Long Answer type Questions9videos
POLYNOMIALS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ANSWER TYPE QUESTIONS12videos
STATISTICS AND PROBABILITY
Similar Questions
ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
View SolutionABCD is a rectangle formed by joining the points A(−1, −1), B(−1, 4), C(5, 4) and D(5, −1). P, Q, R and S are the mid-points of sides AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? a rectangle? or a rhombus? Justify your answer.
View SolutionABCD is a rectangle formed by the points A(1, 1),B(1, 4),C(5, 4) and D(5, 1). P, Q, R and S are the midpoints of AB, BC, CD and DA respectively. Is the quadrilateral PQRS a square? A rectangle? or a rhombus? Justify your answer.
View SolutionABCD is a rhombus and P,Q,R,S are the mid-points of AB,BC,CD,DA respectively. Prove that PQRS is a rectangle.
View SolutionABCD is a rhombus and P, Q, R, S are the mid-points of AB, BC, CD, DA respectively. Prove that PQRS is a rectangle.
View SolutionIn the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.
 View Solution
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.
 View Solution
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR ABCD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionA (-4, 2), B(0, 2) and C(-2,-4) are vertices of a triangle ABC. P, Q and R are mid-points of sides BC, CA and AB respectively. Show that the centroid of Δ PQR is the same as the centroid of Δ ABC.
View SolutionP, Q , R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a rhombus.
View Solution

