ABCD is a rhombus with AC=2BD. Diagonals AC and BD intersect at P.E1,E2,E3andE4 are four ellipes passing through P and their foci are A and B, B and C, C and D and D and A, respectively . If for i=1,2,3,4,ei are the eccentricities fo Ei, then
ei=e3
e2=e4
e1=2e2
e1=e2
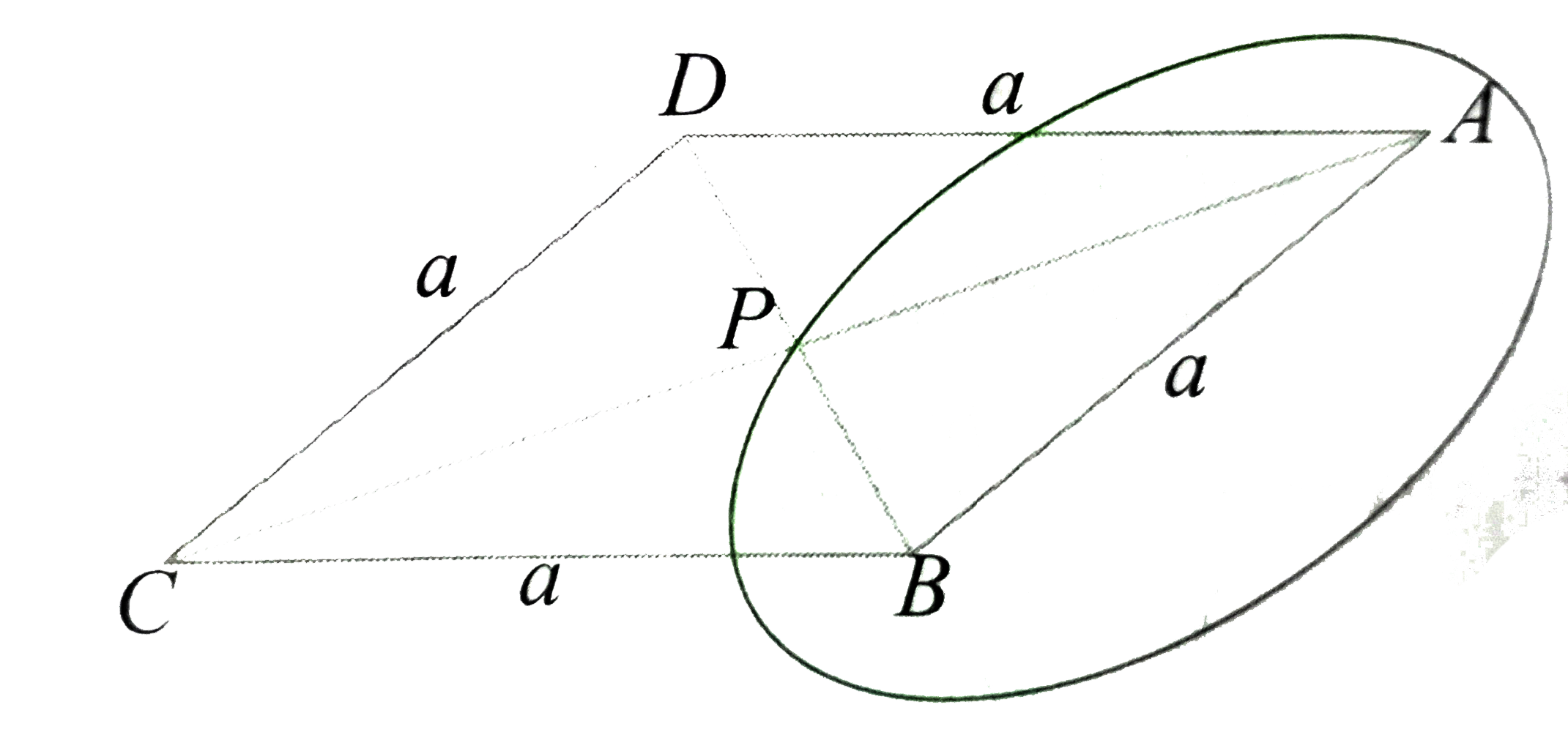
AB=BC=CD=DA=
Since ΔPAB,ΔPBC,ΔPCD,ΔPDA are congruent,
e1=e2=e3=34=aPA+PB
Similar Questions
Knowledge Check
In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
Ax - y - 1 = 0Bx + y - 1 = 0Cx - y + 1 = 0Dx + y - 7 =0In a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
Ax−y−1=0Bx+y−1=0Cx−y+1=0Dx+y−7=0A, B, C, D are four points on a circle. AC and BD intersect at a point E such that ∠BEC=130∘and∠ECD=20∘.∠BAC is
A(A) 120B(B)90∘C(C)100∘D(D)110∘
ABCD is a rhombus. Its diagonals ACandBD intersect at the point M and satisfy BD=2AC.If he point DandM represent the complex numbers 1+iand2−i respectively, then A represents the complex number......or......
View SolutionABCD is a rhombus. Its diagonals ACandBD intersect at the point M and satisfy BD=2AC.If he point DandM represent the complex numbers 1+iand2−i respectively, then A represents the complex number......or......
View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE:EC=BE:ED.
Show that : ABCD is a trapezium.
View Solution
