In quadrilateral ABCD, diagonals AC and BD intersect at point E such that
AE:EC=BE:ED.
Show that : ABCD is a trapezium.
To show that quadrilateral ABCD is a trapezium given that the diagonals AC and BD intersect at point E such that AE : EC = BE : ED, we can follow these steps:
1. Understand the Given Ratio: We are given that AE : EC = BE : ED. This means that the segments created by the intersection of the diagonals are proportional.
2. Set Up Proportions: From the given ratio, we can express it as:
AEEC=BEED
Let AE = x, EC = y, BE = z, and ED = w. Then we can write:
xy=zw
3. Cross Multiply: By cross-multiplying the proportions, we get:
x⋅w=y⋅z
4. Consider Triangles: Now, consider triangles ABE and CDE. We will show that these triangles are similar.
5. Identify Corresponding Angles:
- Angle ABE and angle CDE are vertically opposite angles, hence they are equal.
- Angle AEB and angle CED are also vertically opposite angles, hence they are equal.
6. Apply the Side-Angle-Side (SAS) Similarity Criterion: Since we have:
- Angle ABE = Angle CDE (from step 5)
- AE/EC = BE/ED (from step 2)
We can conclude that triangles ABE and CDE are similar by the SAS similarity criterion.
7. Corresponding Angles: From the similarity of triangles ABE and CDE, we know that:
ABCD=AEEC=BEED
This implies that the angles corresponding to AB and CD are equal.
8. Establish Parallel Lines: Since the angles AB and CD are equal, by the Alternate Interior Angles Theorem, we can conclude that lines AB and CD are parallel.
9. Conclusion: Since we have established that one pair of opposite sides (AB and CD) are parallel, we can conclude that quadrilateral ABCD is a trapezium.
AEEC=BEED
Let AE = x, EC = y, BE = z, and ED = w. Then we can write:
xy=zw
x⋅w=y⋅z
- Angle ABE and angle CDE are vertically opposite angles, hence they are equal.
- Angle AEB and angle CED are also vertically opposite angles, hence they are equal.
- Angle ABE = Angle CDE (from step 5)
- AE/EC = BE/ED (from step 2)
We can conclude that triangles ABE and CDE are similar by the SAS similarity criterion.
ABCD=AEEC=BEED
This implies that the angles corresponding to AB and CD are equal.
Topper's Solved these Questions
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(B)
17 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(C)
24 Videos
- SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)BOOK - ICSECHAPTER - SIMILARITY (WITH APPLICATIONS TO MAPS AND MODELS)EXERCISE - EXERCISE 15(E)
61 Videos
- SIMILARITY BOOK - ICSECHAPTER - SIMILARITY EXERCISE - MULTIPLE CHOICE QUESTIONS (COMPETENCY BASED QUESTIONS)
10 Videos
- SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)BOOK - ICSECHAPTER - SOLVING (SIMPLE) PROBLEMS (BASED ON QUADRATIC EQUATIONS)EXERCISE - Exercise 6(e )
18 Videos
Similar Questions
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
ΔAOB is similar to ΔCOD.
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
OA×OD=OB×OC.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View SolutionIn the adjoining figure, ABCD is a quadrilateral. Its diagonals AC and BD intersect at point 'O'. Prove that :
(a) AB+BC+CD+DA<2(AC+BD)
(b) AB+BC+CD+DA>(AC+BD)

View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,
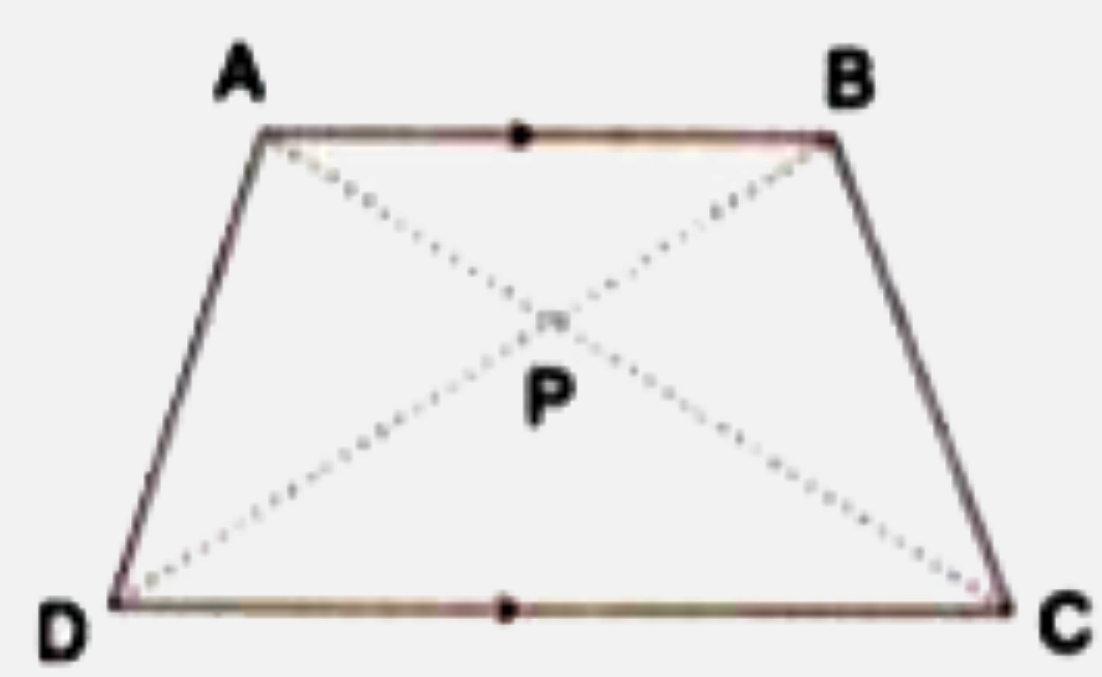
Find :
ΔDPC:ΔAPB
View SolutionThe given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3:5,

Find :
ΔAPB:ΔADB
View SolutionIn quadrilateral ABCD, diagonal BD is bisected by the diagonal AC. Prove that : ΔABCandΔADC are equal in area.
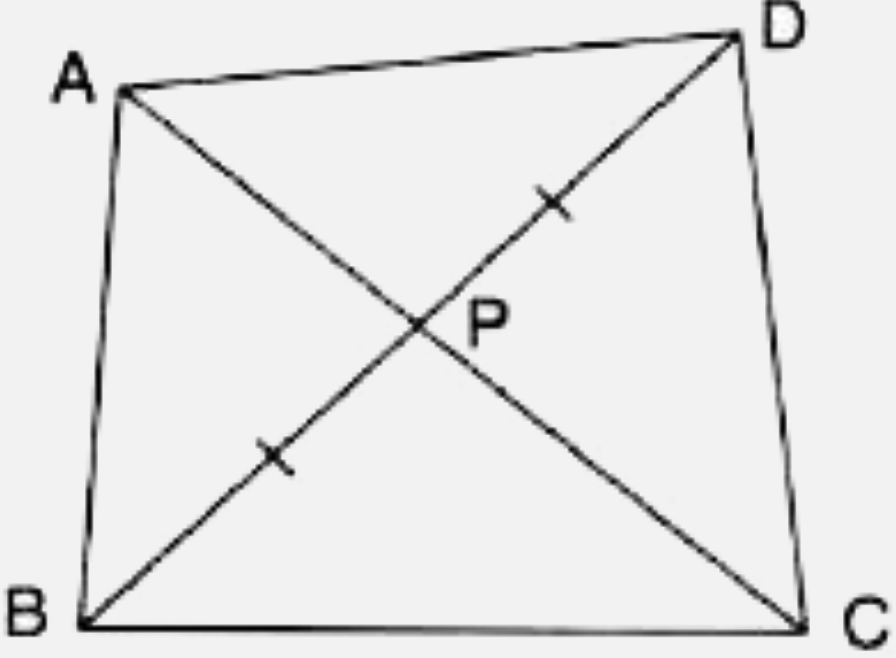
View SolutionIn a rhombus ABCD the diagonals AC and BD intersect at the point (3,4) . If the point A is (1,2) the diagonal BD has the equation
View SolutionIn trapezium ABCD, side AB is parallel to side DC. Diagonals AC and BD intersect at point P. Prove that triangles APD and BPC are equal in area.
View Solution
