ABCD is a square of side . A line parallel to the diagonal BD at a distance 'x' from the vertex A cuts two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x. Find this area at and at , when .
There are two cases
Case -I : when
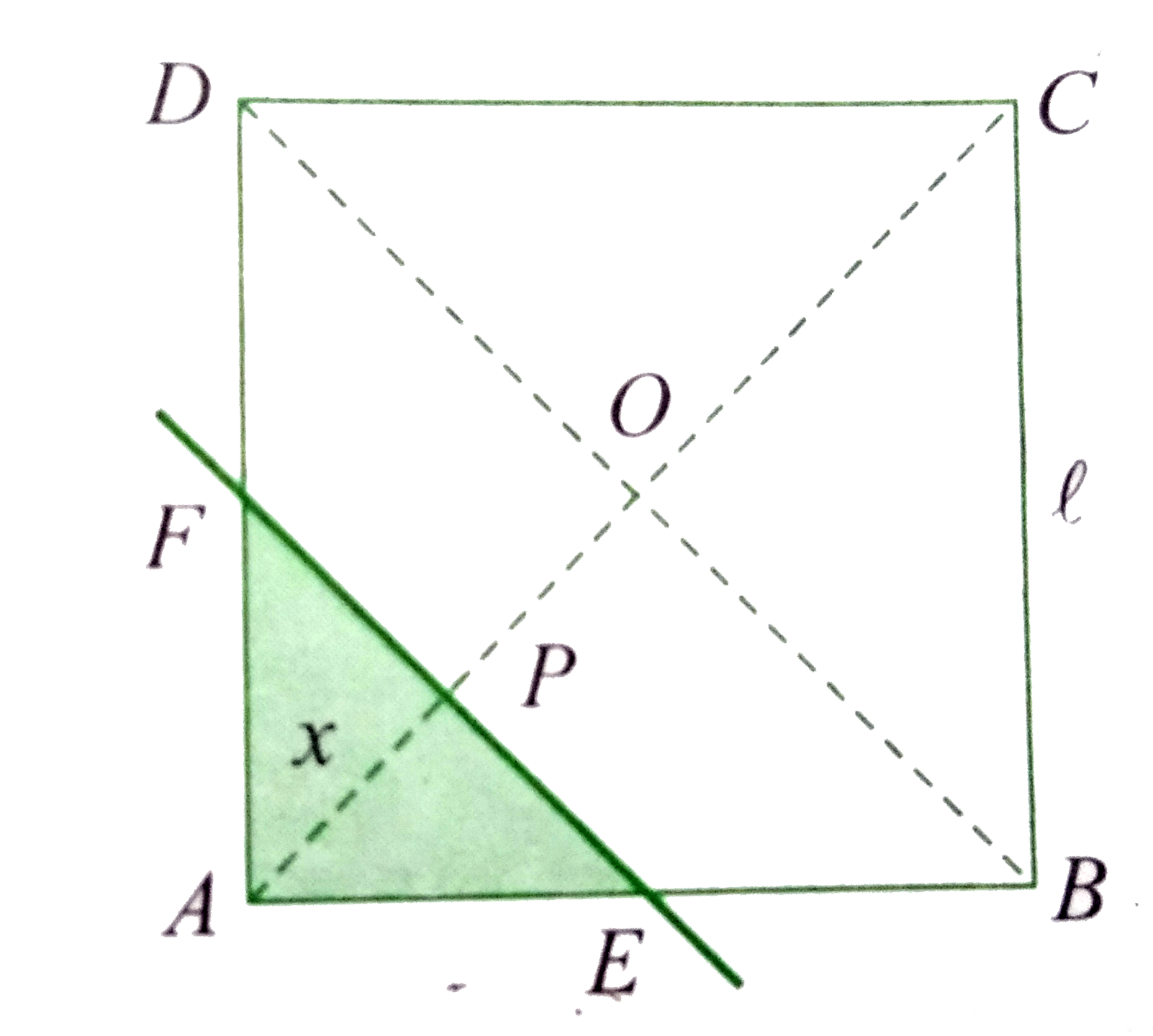
Case-II : when

So, the required function s(x) is
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.1
15 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.2
5 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
ABCD is a square of side a. A line parallel to the diagonal BD at a distance x from the vertex A cuts the two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x.
View SolutionABCD is a square of side a. A line parallel to the diagonal BD at a distance x from the vertex A cuts the two adjacent sides. Express the area of the segment of the square with A at a vertex, as a function of x.
View SolutionIn the figure,ABCD is a square with side x as shown. A parallelogram ABPC is drawn on the side AB as shown. Find the ratio of the area of square to the area of the parallelogram.
View SolutionA rhombus has two of its sides parallel to the lines y=2x+3andy=7x+2. If the diagonals cut at (1, 2) and one vertex is on the y-axis, find the possible values of the coordinate of that vertex.
View SolutionA rhombus has two of its sides parallel to the lines y=2x+3andy=7x+2. If the diagonals cut at (1, 2) and one vertex is on the y-axis, find the possible values of the ordinate of that vertex.
View Solutionxandy are the sides of two squares such that y=x−x2 . Find the rate of the change of the area of the second square with respect to the first square.
View Solutionx and y are the sides of two squares such that y=x−x2 . Find the rate of the change of the area of the second square with respect to the first square.
View Solutionxandy are the sides of two squares such that y=x−x2 . Find the rate of the change of the area of the second square with respect to the first square.
View Solutionxandy are the sides of two squares such that y=x−x2 . Find the rate of the change of the area of the second square with respect to the first square.
View SolutionIf x and y are the sides of two squares such that y=x−x2. Find the change of the area of second square with respect to the area of the first square.
View Solution
