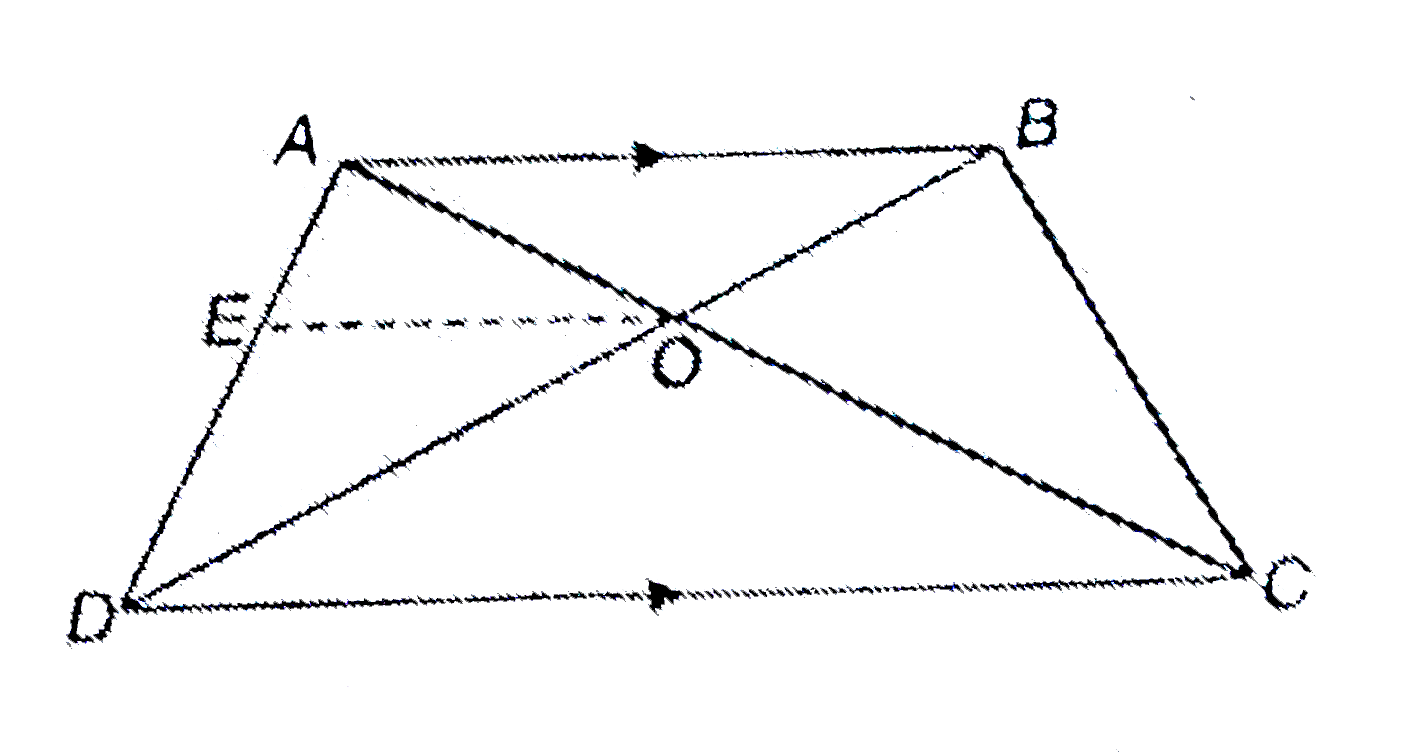
ABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that $\frac{A O}{B O} = \frac{C O}{D O}$ .

Video Solution

Text Solution

Verified by Experts

$I n ∠ A C D$
EO||DC
$\frac{A E}{E D} = \frac{A O}{O C}$ -(1)
$I n ∠ B C D$
OF||DC
$\frac{B O}{O D} = \frac{B F}{F C}$
$I n ∠ A D B$
EO||AB
$\frac{E A}{D E} = \frac{O B}{O D}$
putting this value in equation 1
$\frac{O C}{O B} (\frac{A O}{O C} = \frac{O B}{O D}) \frac{O C}{O B}$
$\frac{A O}{O B} = \frac{O C}{O D}$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A $1 : 4$
B $1 : 2$
C $4 : 1$
D $2 : 1$
Question 2 - Select One
ABCD is a trapezium in which $A B ∣ ∣ C D$ and $A B = 2 C D$ . It its diagonals intersect each other at O then ratio of the area of triangle AOB and COD is
A $1 : 2$
B $2 : 1$
C $1 : 4$
D $4 : 1$
Question 3 - Select One
ABCD is a trapezium in which AB||CD and AB=2CD. If its diagonals intersect each other at O, then ratio of areas of trianlges AOB and COD is :
A1:4
B1:2
C4:1
D2:1

NCERT-TRIANGLES-Exercise 6.2

Home
Ask Doubt
Profile