Question

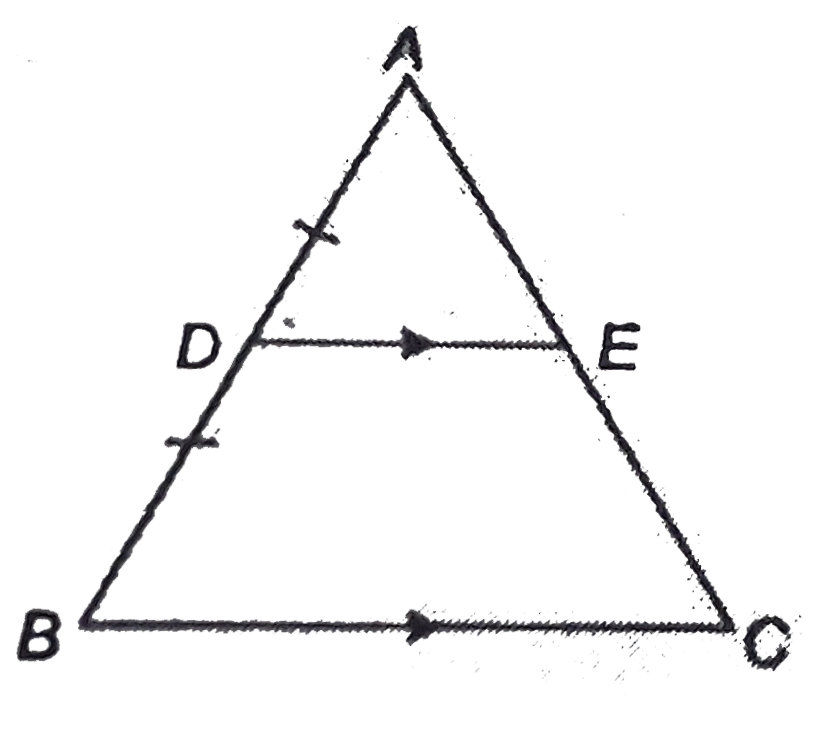
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).

Explanation

To prove that a line drawn through the midpoint of one side of a triangle and parallel to another side bisects the third side, we will use Theorem 6.1.

1. Consider Triangle ABC: Let triangle ABC be given, where we have points A, B, and C.

2. Identify Midpoint: Let P be the midpoint of side AB. This means that AP = PB.

3. Draw a Parallel Line: Draw a line segment PQ through point P that is parallel to side BC.

4. Apply Theorem 6.1: According to Theorem 6.1, if a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally. Thus, we can write the proportion:
\( \frac{AQ}{QC} = \frac{AP}{PB} \)

5. Substitute Midpoint Values: Since P is the midpoint of AB, we have:
\( AP = PB \)
Therefore, we can substitute this into our proportion:
\( \frac{AQ}{QC} = \frac{AP}{AP} = 1 \)

6. Conclude Equal Segments: Since the ratio \(\frac{AQ}{QC} = 1\), it implies that:
\( AQ = QC \)
This means that point Q is the midpoint of side AC.

7. Final Statement: Hence, we have proved that the line segment PQ, drawn through the midpoint P of side AB and parallel to side BC, bisects side AC at point Q.