ABCD is a trapezium with AB//DC. A line parallel to AC intersects Ab at point M and BC at point N. Prove that :
area ofΔADM=area ofΔACN.
To prove that the area of triangle ΔADM is equal to the area of triangle ΔACN in trapezium ABCD where AB∥DC and a line parallel to AC intersects AB at M and BC at N, we can follow these steps:
1. Identify the Trapezium:
Let ABCD be a trapezium with AB∥DC. Draw the diagonals AC and BD.
2. Draw the Parallel Line:
Draw a line parallel to AC that intersects AB at point M and intersects BC at point N.
3. Identify the Triangles:
We need to consider the triangles ΔADM and ΔACN.
4. Use the Area of Triangles Between Parallel Lines:
Since AB∥DC and MN∥AC, we can use the property that triangles formed between two parallel lines with a common base have equal areas.
5. Base and Height Consideration:
Both triangles ΔADM and ΔACN share the same height from point A to line MN because they are between the same parallel lines. The bases of these triangles are AM and AC respectively.
6. Establishing Area Equality:
- The area of triangle ΔADM can be expressed as:
AreaΔADM=12×base×height
where the base is AM and the height is the perpendicular distance from D to line MN.
- The area of triangle ΔACN can be expressed similarly:
AreaΔACN=12×base×height
where the base is AC and the height is the same as above.
7. Conclusion:
Since both triangles share the same height and their bases are proportional due to the parallel lines, we conclude:
AreaΔADM=AreaΔACN
Let ABCD be a trapezium with AB∥DC. Draw the diagonals AC and BD.
Draw a line parallel to AC that intersects AB at point M and intersects BC at point N.
We need to consider the triangles ΔADM and ΔACN.
Since AB∥DC and MN∥AC, we can use the property that triangles formed between two parallel lines with a common base have equal areas.
Both triangles ΔADM and ΔACN share the same height from point A to line MN because they are between the same parallel lines. The bases of these triangles are AM and AC respectively.
- The area of triangle ΔADM can be expressed as:
AreaΔADM=12×base×height
where the base is AM and the height is the perpendicular distance from D to line MN.
- The area of triangle ΔACN can be expressed similarly:
AreaΔACN=12×base×height
where the base is AC and the height is the same as above.
Since both triangles share the same height and their bases are proportional due to the parallel lines, we conclude:
AreaΔADM=AreaΔACN
Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
ABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of ΔADX = area of ΔACY.
View SolutionABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of ΔADX = area of ΔACY.
View Solution
Knowledge Check
ABCD is a trapezium with AB parallel to DC. Then the triangle similar to ΔAOB is:
 AΔADBBΔACBCΔCODDΔCOB
AΔADBBΔACBCΔCODDΔCOB
ABCD is a trapezium with AB∣∣DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔOBD)= area (ΔOCE)
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔACD)= area (ΔABE)
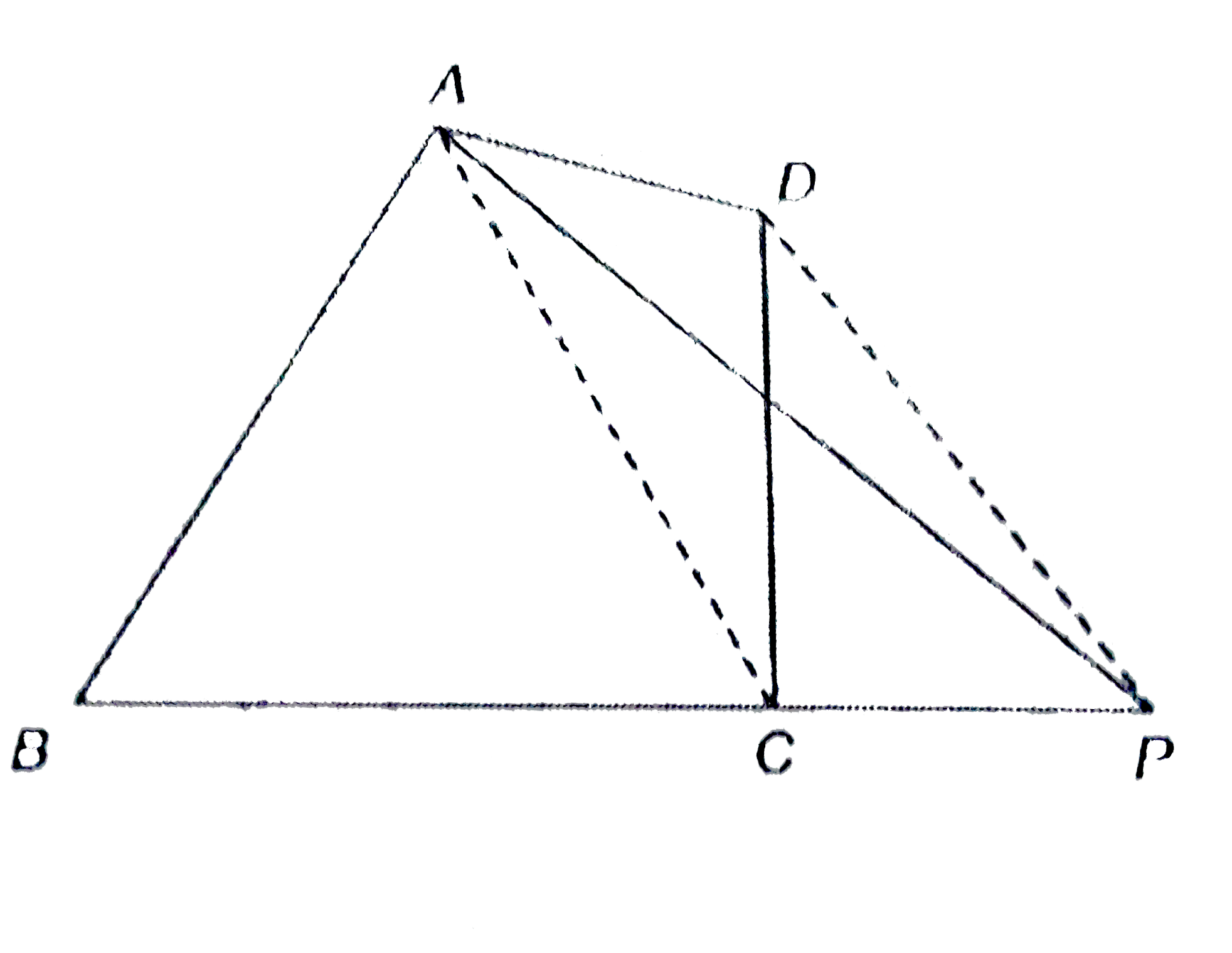
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
are of ΔABP= area of □ABCD
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View Solution
