ABCD is a trapezium with AB//DC. A line parallel to AC intersects Ab at point M and BC at point N. Prove that :
area ofΔADM=area ofΔACN.
Step by step video & image solution for ABCD is a trapezium with AB////DC. A line parallel to AC intersects Ab at point M and BC at point N. Prove that : "area of" DeltaADM= "area of" DeltaACN. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(B)
16 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA THEOREMSBOOK - ICSECHAPTER - AREA THEOREMSEXERCISE - Exercies 16(C )
22 Videos
- AREA AND PERIMETER OF PLANE FIGURESBOOK - ICSECHAPTER - AREA AND PERIMETER OF PLANE FIGURESEXERCISE - EXERCISE 20(D)
12 Videos
- CHAPTER REVISION (STAGE 2) BOOK - ICSECHAPTER - CHAPTER REVISION (STAGE 2) EXERCISE - DISTANCE FORMULA
12 Videos
Similar Questions
ABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of ΔADX = area of ΔACY.
View SolutionABCD is a trapezium with AB parallel to DC. A line parallel to AC intersects AB at X and BC at Y. Prove that area of ΔADX = area of ΔACY.
View Solution
Knowledge Check
ABCD is a trapezium with AB parallel to DC. Then the triangle similar to ΔAOB is:
 AΔADBBΔACBCΔCODDΔCOB
AΔADBBΔACBCΔCODDΔCOB
ABCD is a trapezium with AB∣∣DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ADX) = ar (ACY).
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔOBD)= area (ΔOCE)
View SolutionIn ΔABC ,D is a point in side AB and E is a point in AC. If DE is parallel to BC, and BE and CD intersect each other at point 0, prove that:
area (ΔACD)= area (ΔABE)
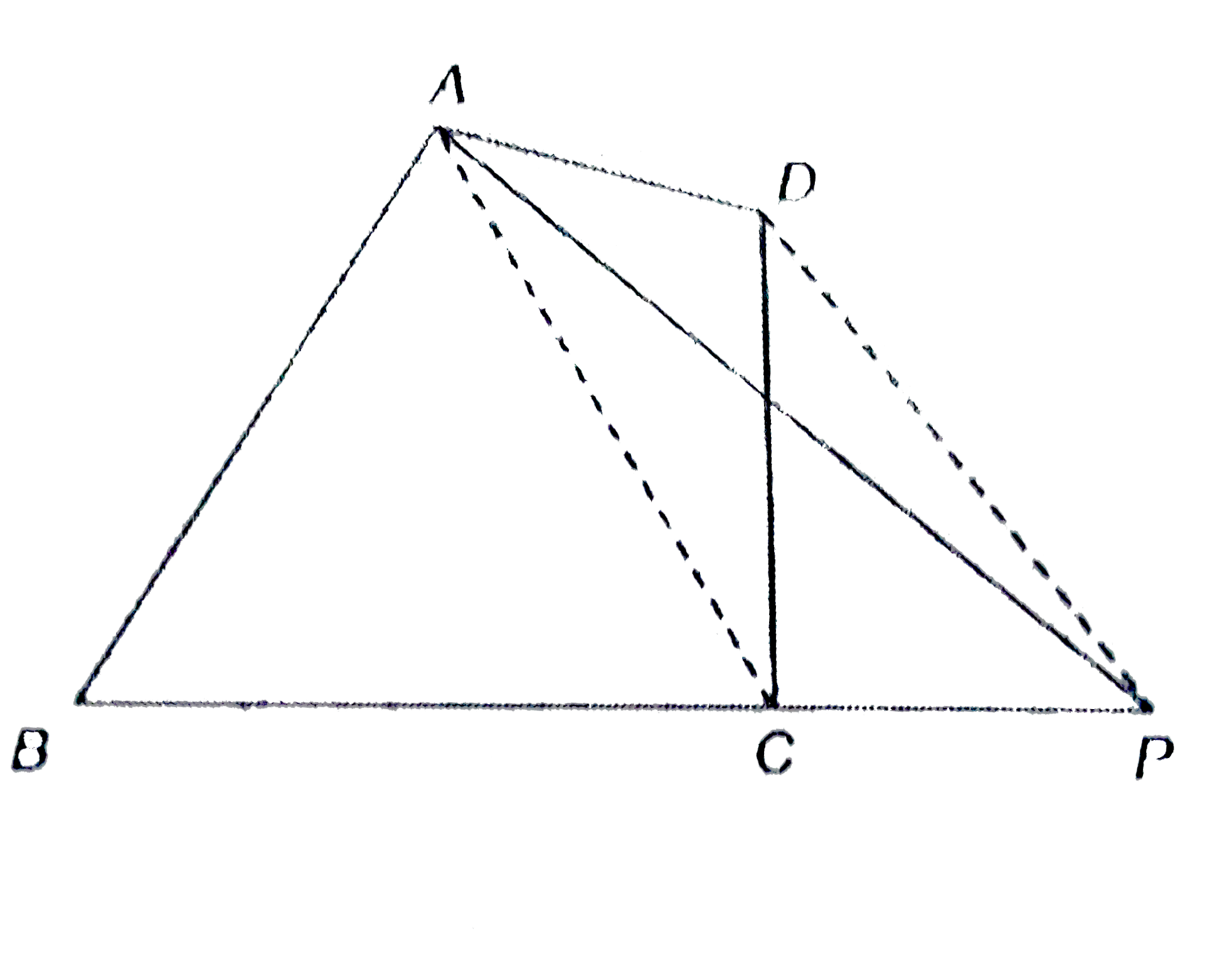
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
are of ΔABP= area of □ABCD
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionIn a trapezium ABCD, AB/DC, E is mid-point of aD. A line through E and parallel to AB intersects BC at point F. Show that:
2EF=AB+DC
View Solution
