about to only mathematics Solution in Tamil
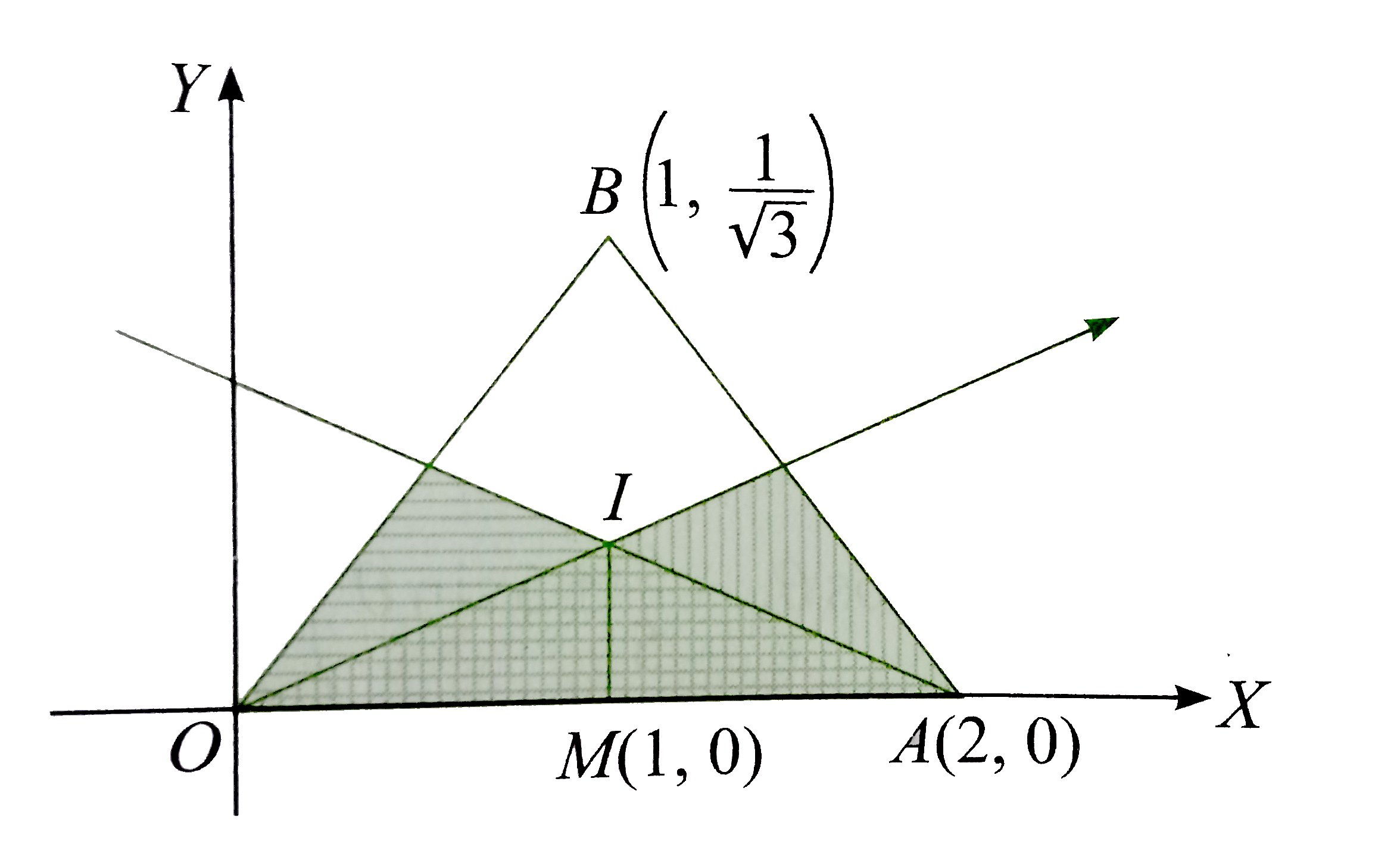
d(P,OA)≤ min[d(P,OB),d(P,AB)],
⇒d(P,OA)≤d(P,OB)and d(P,OA)≤d(P,AB),
When d(P,OA)= d(P,OB), P is equidistant from OA and OB, i.e., P lies on angle bisector of lines OA and OB.
So, when d(P,OA)<d(P,OB), Point P is nearer to OA than to OB, i.e., it lies below bisector of OA and oB.
Similarly, when d(P,OA)<d(P,AB) P is nearer to OA than to AB, i.e., it lies below bisector of OA and AB.
Common region satisfied by these two inequalities is the region formed by two bisectors and OA, i.e., triangle OIA.
∴ Required area = Area of triangle OIA
Now, ∠BOA=1/√31=1√3
∴∠BOA=30∘
⇒∠IOA=15∘
⇒IM=tan15∘=2−√3
∴Area of triangle OIA=12×OA×IM
=12×2×(2−√3)=2−√3 sq. units
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.1
23 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
Find the equation of the right bisector of the line segment joining the points (3,4) and (−1,2).
View SolutionFind the points on the line x + y = 1 that lie at a distance 3 units from the line 5x+12y = 3.
View SolutionThe point P(α,α+1) will lie inside the triangle whose vertices are A(0,3),B(−2,0) and C(6,1) if
View SolutionQ. Let p and q real number such that p≠0,p2≠q and p2≠−q. if α and β are non-zero complex number satisfying α+β=−p and α3+β3=q, then a quadratic equation having αβ and βα as its roots is
View SolutionWhat did Schimba say about mathematics?
View SolutionWhich of the following statements is not true about 'mapping in Mathematics?
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solutionabout to only mathematics
View Solution
