AD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
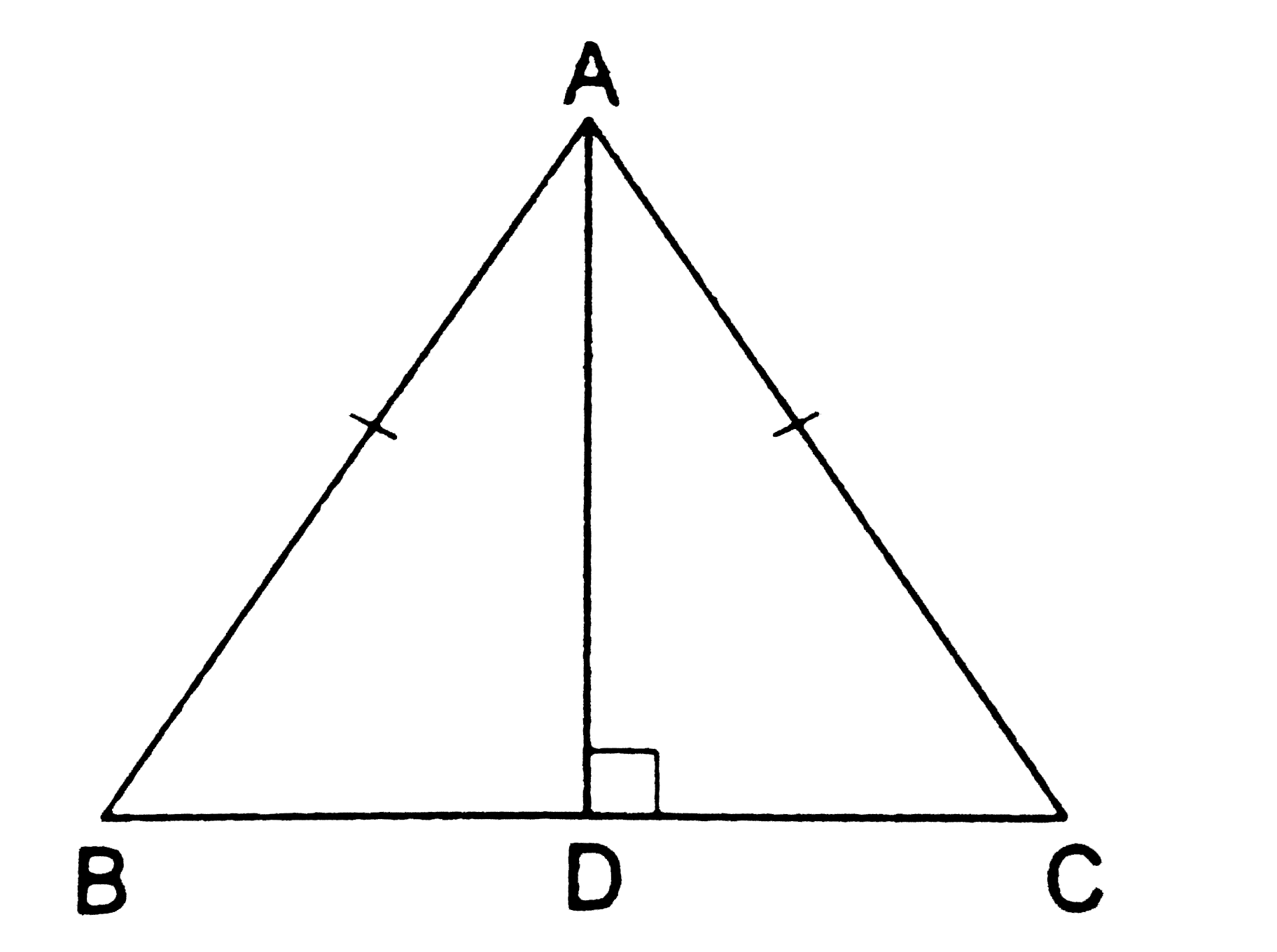

(i) In ΔBAD and ΔCAD,
∠ADB=∠ADC (Each 90∘as AD is an altitude)
AB=AC (Given)
AD=AD (Common)
∴ ΔBAD≅ΔCAD (By RHS Congruence rule)
∴ BD=CD (By CPCT)
Hence, AD bisects BC.
(ii) Since,ΔBAD≅ΔCAD
By CPCT, ∠BAD=∠CAD
Hence, AD bisects ∠A.
Similar Questions
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
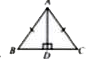
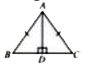
AD bisects BCView SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
AD bisects ∠AView SolutionFind the length of altitude AD of an isosceles ΔABC in which AB=AC=2a units and BC=a units.
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn the adjoining figure, ABC is an isosceles triangle in which AB = AC. Also, D is a point such that BD = CD. Prove that AD bisects ∠A and ∠D
View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal AD bisects ∠B
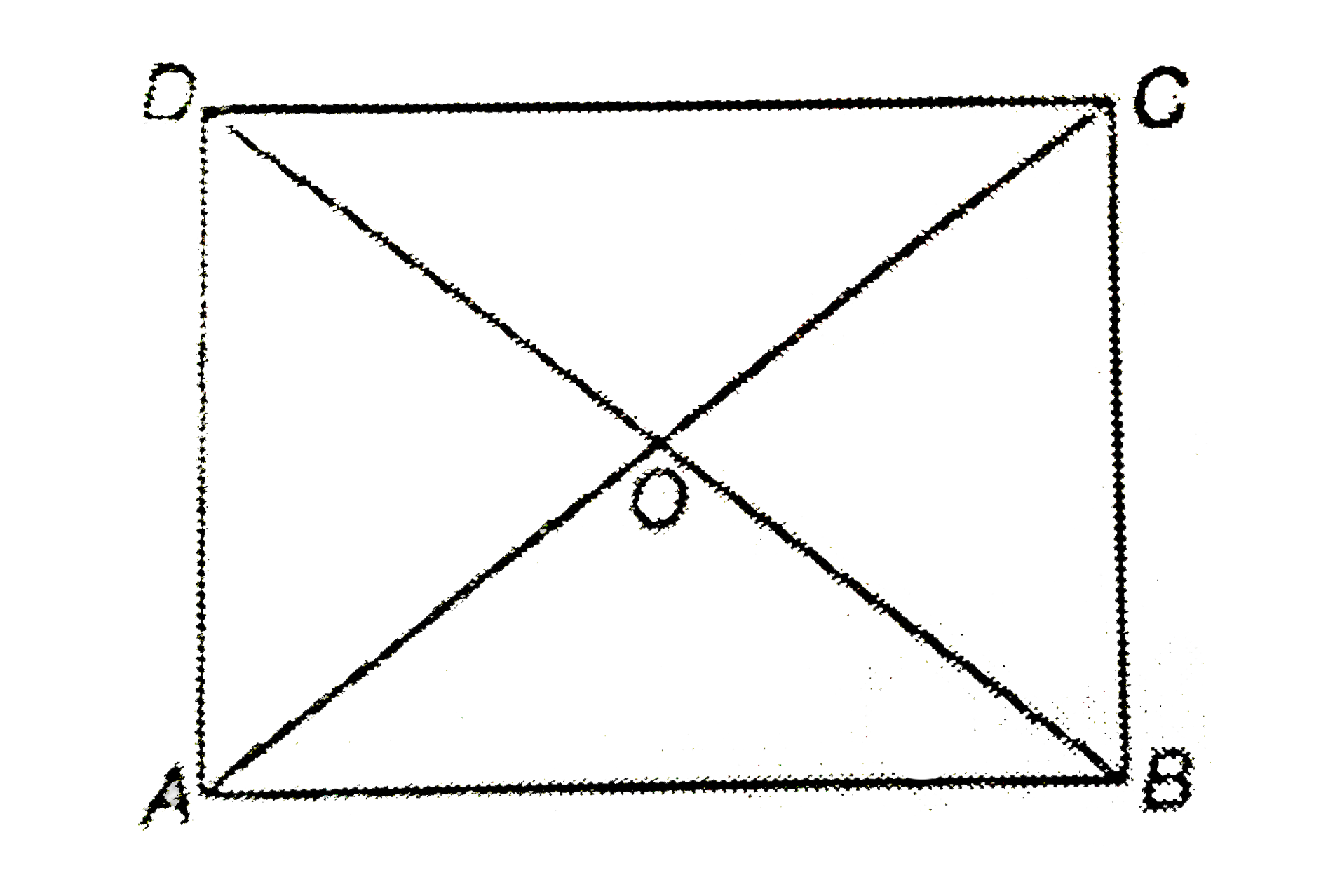 View Solution
View SolutionIn an isosceles ΔABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
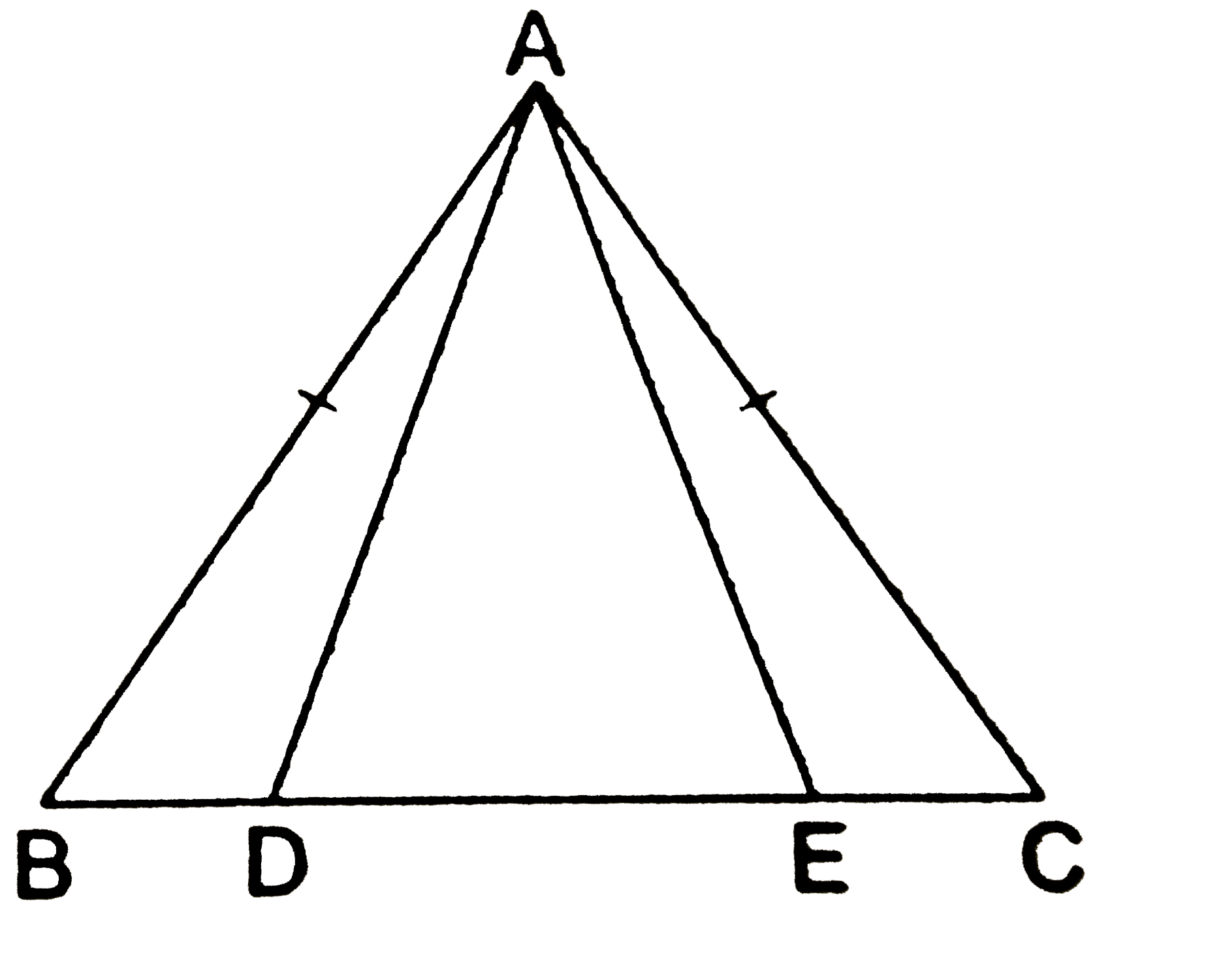 View Solution
View SolutionABCD is a quadrilateral in which AB=BC and AD =CD ,Show that BD bisects boht the angle ABC and ADC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
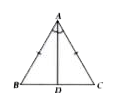
∠B=∠CView SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
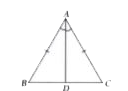
ΔADB≅ΔADCView Solution

