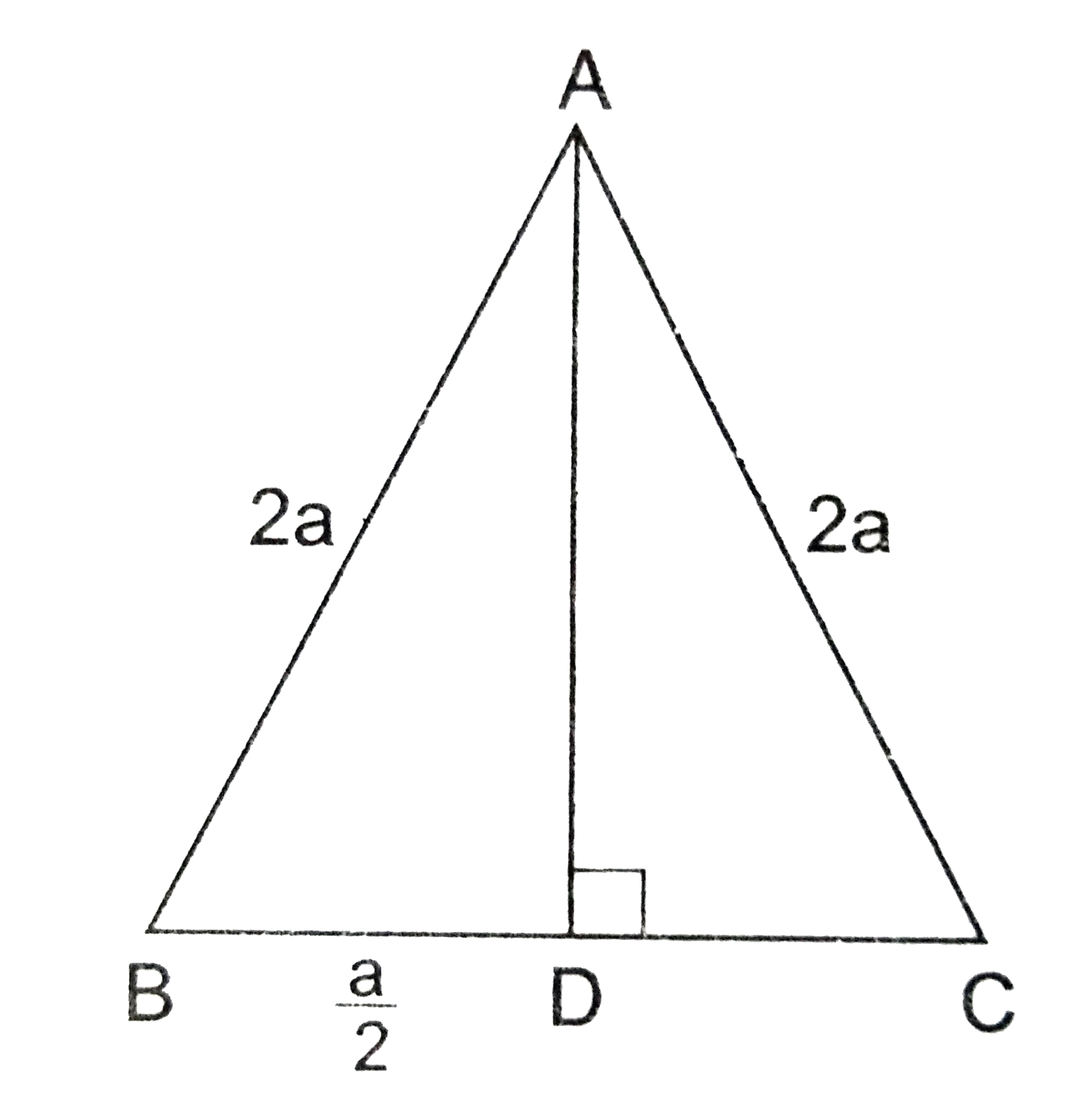
Find the length of altitude AD of an isosceles ΔABC in which AB=AC=2a units and BC=a units.
The correct Answer is:√152 units
In ΔABC,AB=AC=2aandBC=a
Draw AD⊥BC. Then, D is the midpoint of BC and so BD=a2
AD2=AB2−BD2=4a2−a24=15a24⇒AD=a√152
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7E30videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Multiple Choice Questions (Mcq)53videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7C13videos
TRIANGLES
- BOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 1127videos
T-RATIOS OF SOME PARTICULAR ANGLES
- BOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself20videos
TRIGONOMETRIC IDENTITIES
Similar Questions
Knowledge Check
- Question 1 - Select One
In an isosceles ΔABC, if AC=BC and AB2=2AC2 then ∠C=?
A30∘B45∘C60∘D90∘ - Question 2 - Select One
In the given figure, △ABC is an isosceles triangle, in which AB=AC, AD⊥BC, BC = 6cm and AD = 4cm. The length of AB is:
दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD⊥BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ? A4 cmB6 cmC7 cmD5 cm
A4 cmB6 cmC7 cmD5 cm
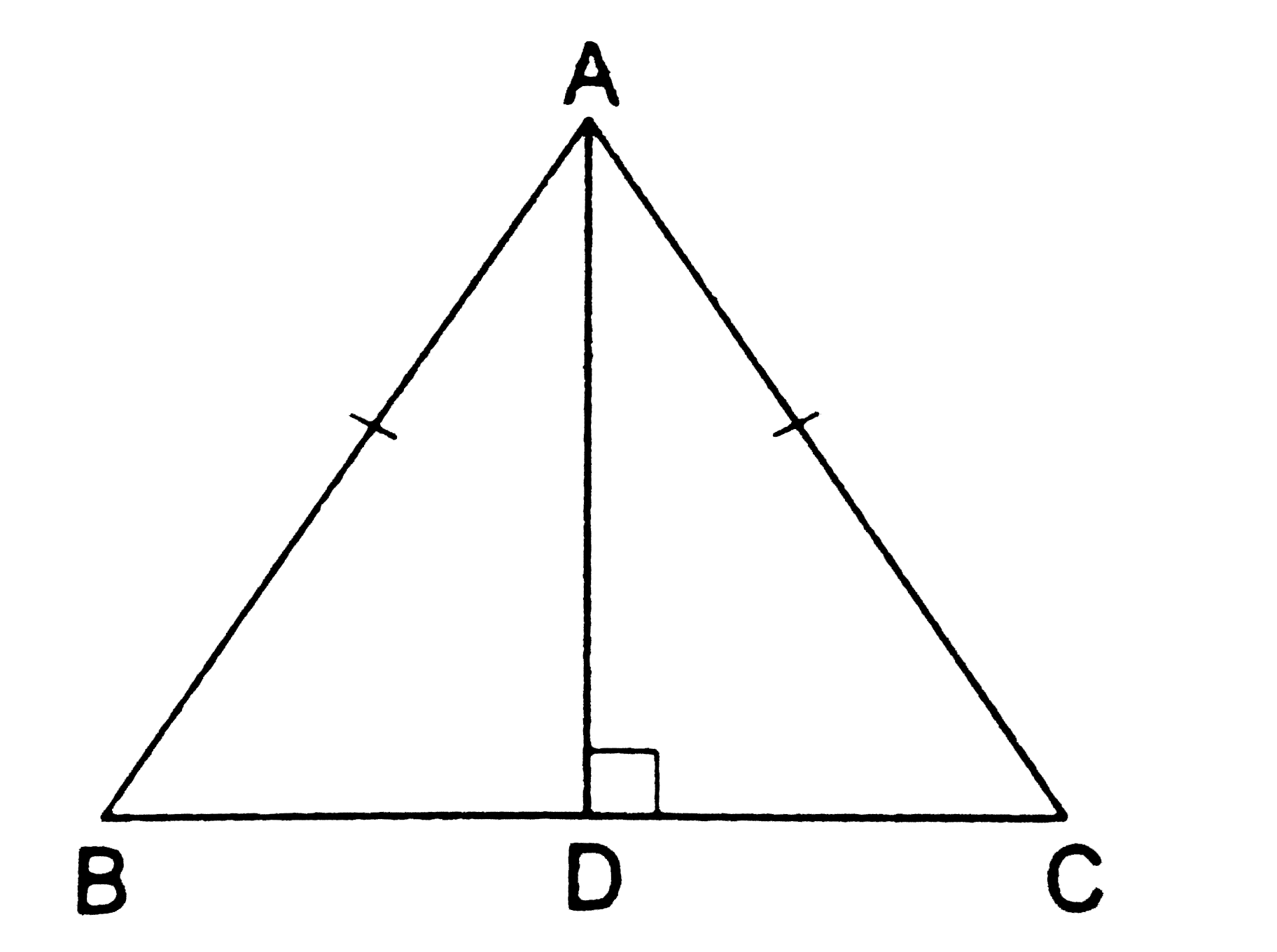
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
AD bisects ∠AView SolutionAD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
 View Solution
View SolutionIn the given figure, △ABC is an isosceles triangle, in which AB=AC, AD⊥BC, BC = 6cm and AD = 4cm. The length of AB is:
दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD⊥BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ? View Solution
View SolutionIn figure, AD and BE are respectively altitudes of an isosceles triangle ABC with AC=BC . Prove that AE=BD.
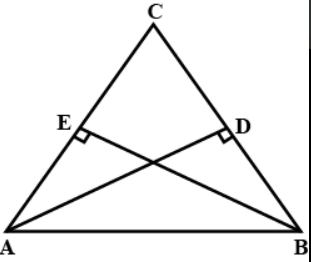 View Solution
View SolutionIn the figure, ABC is an isosceles triangle in which AB = AC and LM is parallel to BC. If ∠A=50∘ find ∠LMC.
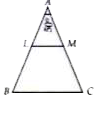 View Solution
View SolutionFind length of AD in ΔABC if AB = 5 AC = 6 and BC = 8
View Solution