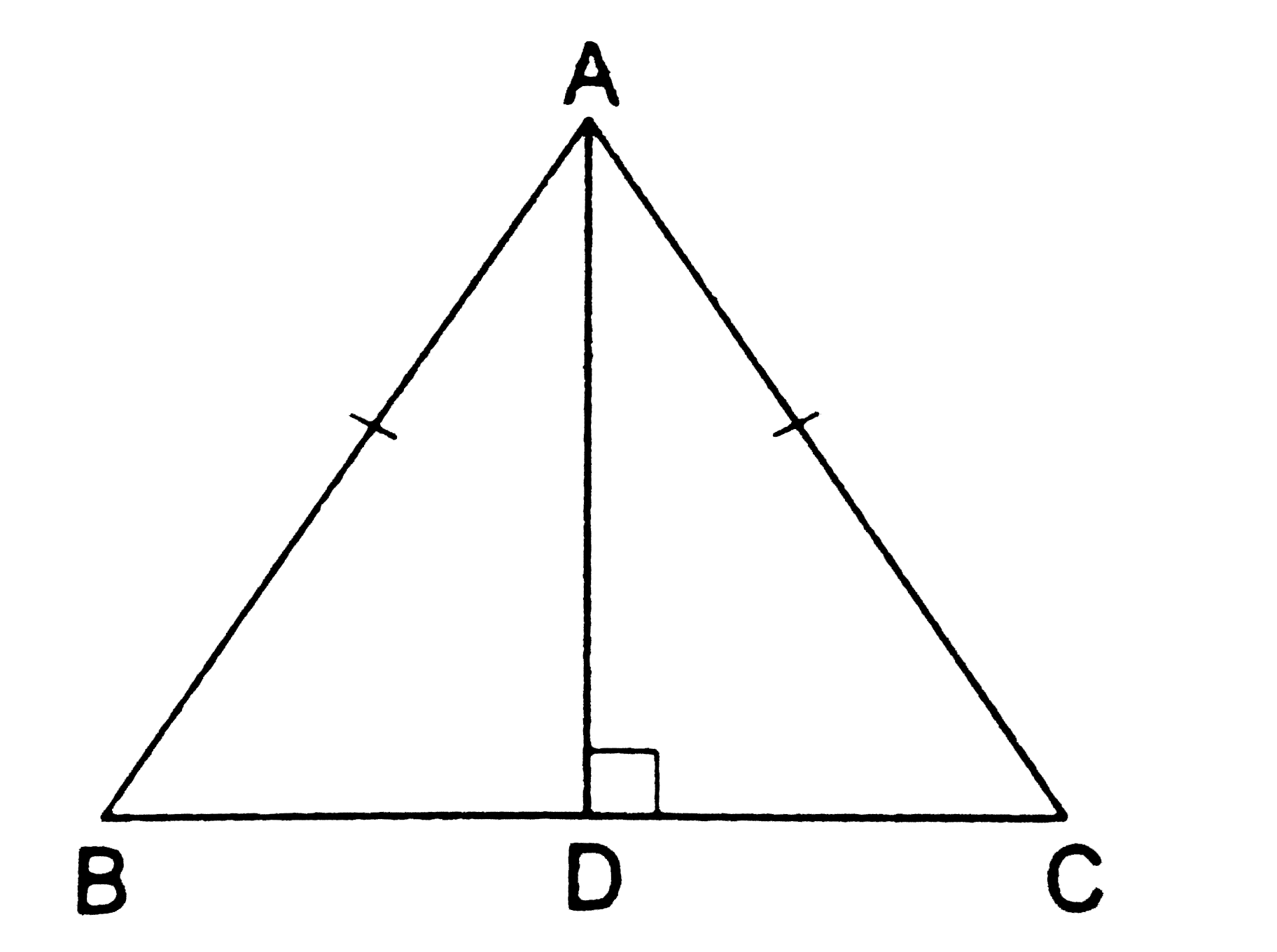
AD is an altitude of an isosceles ΔABC in which AB = AC.
Show that (i) AD bisects BC,
(ii) AD bisects ∠A.
(##IX07_E0302_s01##)
(i) In ΔBAD and ΔCAD,
∠ADB=∠ADC (Each 90∘as AD is an altitude)
AB=AC (Given)
AD=AD (Common)
∴ ΔBAD≅ΔCAD (By RHS Congruence rule)
∴ BD=CD (By CPCT)
Hence, AD bisects BC.
(ii) Since,ΔBAD≅ΔCAD
By CPCT, ∠BAD=∠CAD
Hence, AD bisects ∠A.
Similar Questions
AD is altitude of an isosceles triangle ABC in which AB = AC = 30 cm and BC = 36 cm. A point O is marked on AD in such a way that ∠BOC=90∘. Find the area of quadrilateral ABOC.
View SolutionThe tangent to the circumcircle of an isosceles ΔABC at A, in which AB= AC, is parallel to BC.
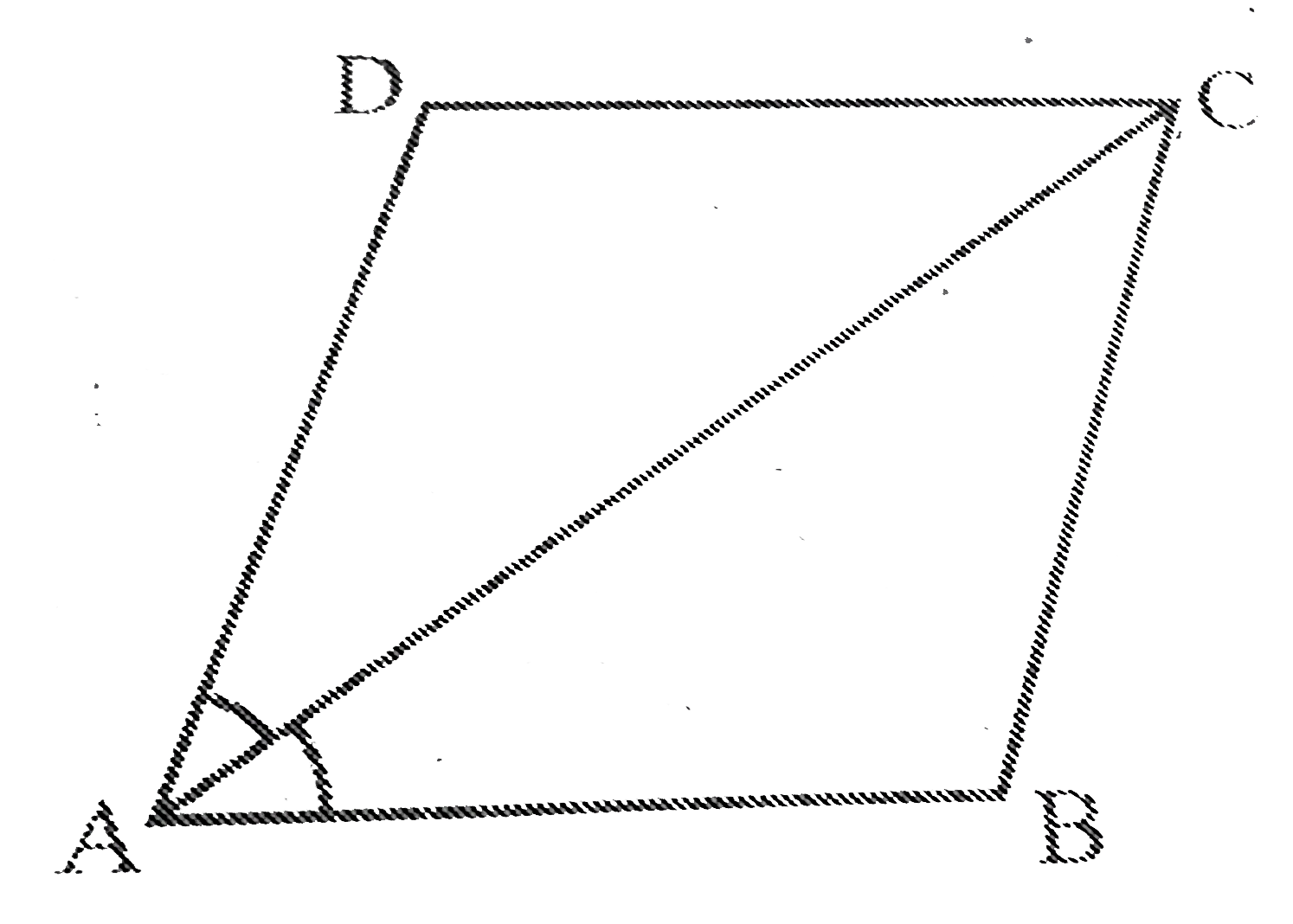
View SolutionDiagonal AC of a parallelogram ABCD bisects ∠A. Show that
(i) it bisects ∠C also,
(ii) ABCD is a rhombus.
 View Solution
View SolutionIn ΔABC,AB=AC and D is a point in BC so that BD=CD. Prove that AD bisects ∠BAC.
View SolutionIn a triangle ABC, AB = AC. Show that the altitude AD is median also.
View SolutionABCD is a quadrilateral in which AB=BC and AD=CD ,Show that BD bisects both the ∠ABC and ∠ADC.
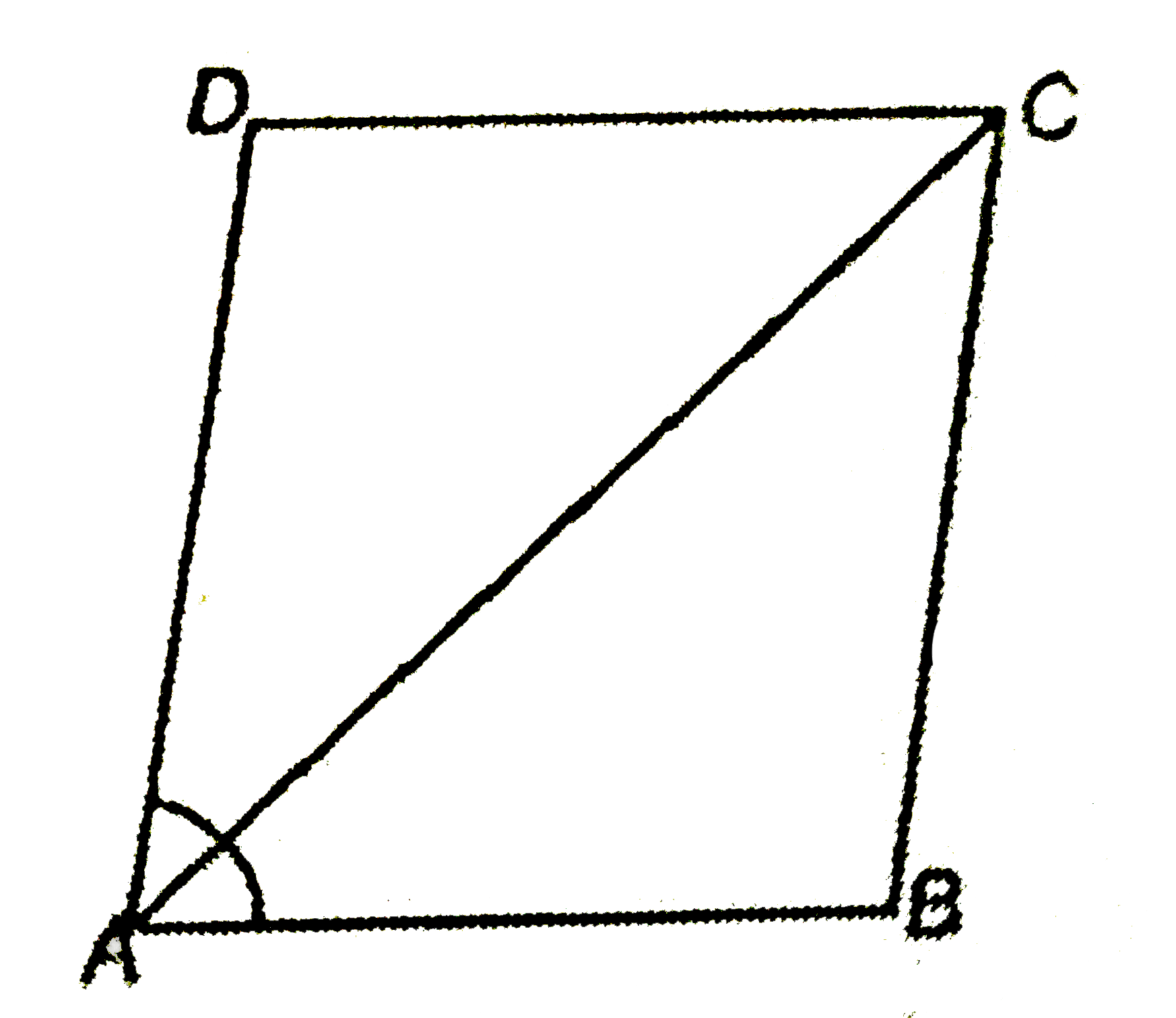
View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B
 View Solution
View SolutionGiven a ΔABD in which AB=AD and AC bisects BD. Prove that :
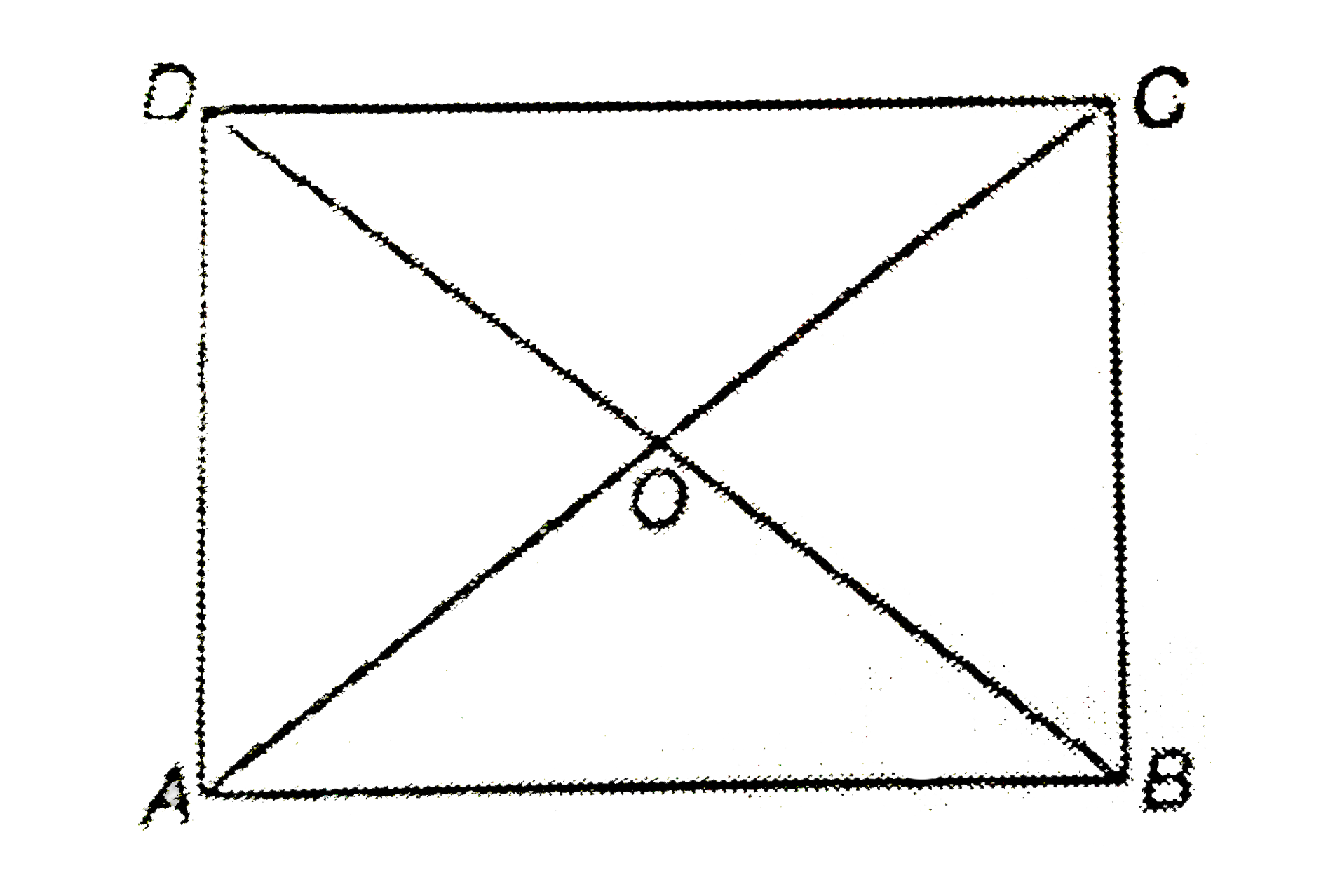
ΔABC≅ΔADC.View SolutionDiagonal AC of a paraleligram ABCD bisects ∠A (sec figure). Show that:
(i) it bisects ∠C also (ii) ABCD is a rhombus.
 View Solution
View SolutionIn the adjoining figure, ΔABC is an isosceles triangles in which AB=AC and AD is the bisector of ∠A. Prove that :
(i) ΔADB≅ΔADC
(ii) ∠B=∠C
(iii) BD=DC
(iv) AD⊥BC
 View Solution
View Solution

