All squares are ___. (congruent/similar)
To solve the question "All squares are ___ (congruent/similar)", we need to understand the definitions of the terms "congruent" and "similar" in the context of geometric figures.
1. Understand the term "congruent":
- Two figures are said to be congruent if they are identical in shape and size. This means that all corresponding sides and angles are equal.
2. Analyze squares:
- A square is defined as a quadrilateral with all four sides equal and all four angles equal (each measuring 90 degrees).
- However, squares can have different side lengths. For example, one square might have a side length of 2 cm, while another might have a side length of 5 cm.
3. Determine if all squares are congruent:
- Since squares can have different side lengths, they cannot be congruent to each other. Therefore, the statement "all squares are congruent" is false.
4. Understand the term "similar":
- Two figures are said to be similar if they have the same shape but not necessarily the same size. This means that their corresponding angles are equal, and the lengths of corresponding sides are in proportion.
5. Determine if all squares are similar:
- All squares have the same shape (four equal sides and four right angles). Therefore, regardless of their size, all squares are similar to each other.
6. Conclusion:
- Since all squares have the same shape, the correct answer to fill in the blank is "similar".
Final Answer:
All squares are similar.
- Two figures are said to be congruent if they are identical in shape and size. This means that all corresponding sides and angles are equal.
- A square is defined as a quadrilateral with all four sides equal and all four angles equal (each measuring 90 degrees).
- However, squares can have different side lengths. For example, one square might have a side length of 2 cm, while another might have a side length of 5 cm.
- Since squares can have different side lengths, they cannot be congruent to each other. Therefore, the statement "all squares are congruent" is false.
- Two figures are said to be similar if they have the same shape but not necessarily the same size. This means that their corresponding angles are equal, and the lengths of corresponding sides are in proportion.
- All squares have the same shape (four equal sides and four right angles). Therefore, regardless of their size, all squares are similar to each other.
- Since all squares have the same shape, the correct answer to fill in the blank is "similar".
All squares are similar.
Similar Questions
Fill in the blanks using the correct word given in bracket: (i) All circles are______(congruent, similar)
(ii) All squares are_____. (similar, congruent)
(iii) All______triangles are similar, (isosceles, equilateral)
(iv) Two polygons of the same number of sides are similar, if
(a) their- corresponding angles are___and
(b) their- corresponding sides are__(equal, proportional)
View SolutionWhich of the following statements are true and which are false;
All squares are congruent.
If two squares have equal areas, they are congruent.
If two rectangles have equal areas, they are congruent.
If two triangles have equal areas, they are congruent.
View Solution
Knowledge Check
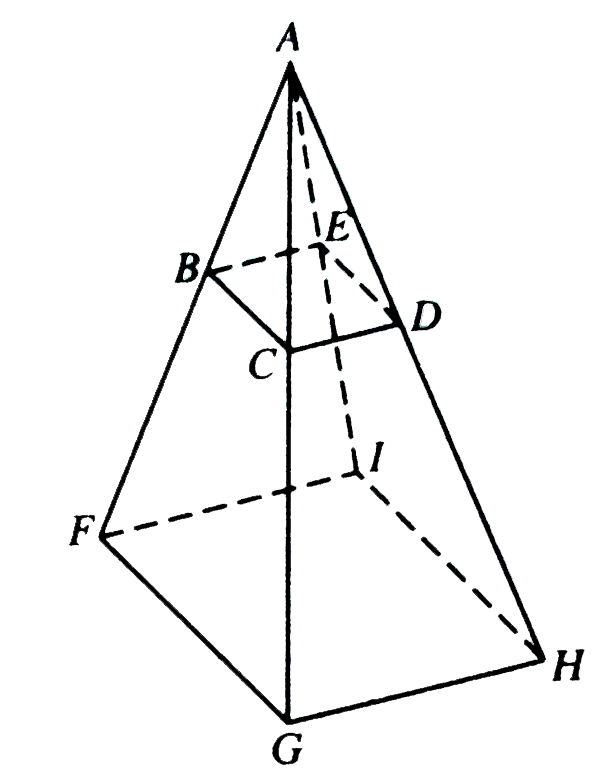
The pyramid in the figure above has square base FGHI , and all triangular faces are congruent. The base BCDE of the small pyramid is also square , and is parallel to FGHI. If the ratio of the area of square BCDE to the area of square FGHI is 1:4 , what is the ratio of the volume of the small pyramid to the volume of the large pyramid ?A1:2B1:3C1:4D1:8
Fill in the blanks: Two square are congruent if
Two rectangles are congruent if
Two circles are congruent if
View SolutionFill in the blanks using the correct word given in brackets: (a) All circles are ................... (congruent, similar) (b) All squares are ................... (similar, congruent) (c) All ....................... triangles are similar (isosceles, equilaterals):
View SolutionIn a squared sheet, draw two triangles of equal areas such that(i) the triangles are congruent.(ii) the triangles are not congruent.What can you say about their perimeters?
View SolutionState, true or false :
All equiangular triangles are similar.
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
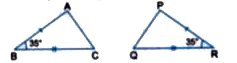
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.
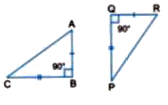
View SolutionState giving reasons, which of the following are pairs of congruent triangles. Write down the names of triangles with congruent sign in each case, wherever they are congruent.

View Solution
