In a squared sheet, draw two triangles of equal areas such that(i) the triangles are congruent.(ii) the triangles are not congruent.What can you say about their perimeters?
To solve the problem of drawing two triangles of equal areas such that (i) the triangles are congruent and (ii) the triangles are not congruent, we will follow these steps:
Step 1: Draw Congruent Triangles
1. Draw Triangle ABC: Let's create a right-angled triangle ABC with sides of lengths 5 cm, 4 cm, and 3 cm.
- Base (AB) = 4 cm
- Height (AC) = 3 cm
- Hypotenuse (BC) can be calculated using the Pythagorean theorem:
BC=√AB2+AC2=√42+32=√16+9=√25=5 cm
2. Draw Triangle PQR: Since the triangles are congruent, we will draw triangle PQR with the same side lengths:
- Base (PQ) = 4 cm
- Height (PR) = 3 cm
- Hypotenuse (QR) = 5 cm
Step 2: Verify Congruence
- By the SSS (Side-Side-Side) congruence rule, triangle ABC is congruent to triangle PQR because all corresponding sides are equal:
Triangle ABC≅Triangle PQR
Step 3: Calculate the Perimeter of Congruent Triangles
- The perimeter of triangle ABC:
Perimeter=AB+AC+BC=4+3+5=12 cm
- The perimeter of triangle PQR is the same:
Perimeter=PQ+PR+QR=4+3+5=12 cm
Step 4: Draw Non-Congruent Triangles
1. Draw Triangle ABC: Let's create another triangle ABC with a base of 3 cm and a height of 4 cm.
- Base (AB) = 3 cm
- Height (AC) = 4 cm
- Hypotenuse (BC) can be calculated:
BC=√AB2+AC2=√32+42=√9+16=√25=5 cm
2. Draw Triangle PQR: Now, we will draw triangle PQR with a base of 2 cm and a height of 6 cm.
- Base (PQ) = 2 cm
- Height (PR) = 6 cm
- Hypotenuse (QR) can be calculated:
QR=√PQ2+PR2=√22+62=√4+36=√40≈6.32 cm
Step 5: Verify Non-Congruence
- The areas of both triangles must be equal:
- Area of triangle ABC:
Area=12×Base×Height=12×3×4=6 cm2
- Area of triangle PQR:
Area=12×Base×Height=12×2×6=6 cm2
- Thus, both triangles have equal areas but are not congruent because their corresponding sides are not equal.
Step 6: Calculate the Perimeter of Non-Congruent Triangles
- The perimeter of triangle ABC:
Perimeter=AB+AC+BC=3+4+5=12 cm
- The perimeter of triangle PQR:
Perimeter=PQ+PR+QR=2+6+√40≈2+6+6.32=14.32 cm
Conclusion
- The perimeters of the congruent triangles (ABC and PQR) are equal (12 cm).
- The perimeters of the non-congruent triangles (ABC and PQR) are different (12 cm and approximately 14.32 cm).
1. Draw Triangle ABC: Let's create a right-angled triangle ABC with sides of lengths 5 cm, 4 cm, and 3 cm.
- Base (AB) = 4 cm
- Height (AC) = 3 cm
- Hypotenuse (BC) can be calculated using the Pythagorean theorem:
BC=√AB2+AC2=√42+32=√16+9=√25=5 cm
- Base (PQ) = 4 cm
- Height (PR) = 3 cm
- Hypotenuse (QR) = 5 cm
- By the SSS (Side-Side-Side) congruence rule, triangle ABC is congruent to triangle PQR because all corresponding sides are equal:
Triangle ABC≅Triangle PQR
- The perimeter of triangle ABC:
Perimeter=AB+AC+BC=4+3+5=12 cm
- The perimeter of triangle PQR is the same:
Perimeter=PQ+PR+QR=4+3+5=12 cm
1. Draw Triangle ABC: Let's create another triangle ABC with a base of 3 cm and a height of 4 cm.
- Base (AB) = 3 cm
- Height (AC) = 4 cm
- Hypotenuse (BC) can be calculated:
BC=√AB2+AC2=√32+42=√9+16=√25=5 cm
- Base (PQ) = 2 cm
- Height (PR) = 6 cm
- Hypotenuse (QR) can be calculated:
QR=√PQ2+PR2=√22+62=√4+36=√40≈6.32 cm
- The areas of both triangles must be equal:
- Area of triangle ABC:
Area=12×Base×Height=12×3×4=6 cm2
- Area of triangle PQR:
Area=12×Base×Height=12×2×6=6 cm2
- Thus, both triangles have equal areas but are not congruent because their corresponding sides are not equal.
- The perimeter of triangle ABC:
Perimeter=AB+AC+BC=3+4+5=12 cm
- The perimeter of triangle PQR:
Perimeter=PQ+PR+QR=2+6+√40≈2+6+6.32=14.32 cm
- The perimeters of the congruent triangles (ABC and PQR) are equal (12 cm).
- The perimeters of the non-congruent triangles (ABC and PQR) are different (12 cm and approximately 14.32 cm).
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLESBOOK - NCERT ENGLISHCHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - EXERCISE 7.1
4 Videos
- CONGRUENCE OF TRIANGLESBOOK - NCERT ENGLISHCHAPTER - CONGRUENCE OF TRIANGLESEXERCISE - SOLVED EXAMPLES
9 Videos
- COMPARING QUANTITIESBOOK - NCERT ENGLISHCHAPTER - COMPARING QUANTITIESEXERCISE - EXERCISE 8.2
10 Videos
- DATA HANDLINGBOOK - NCERT ENGLISHCHAPTER - DATA HANDLINGEXERCISE - EXERCISE 3.2
5 Videos
Similar Questions
If the areas of two similar triangles are equal, prove that they are congruent.
View SolutionIf the areas of two similar triangles are equal, prove that they are congruent.
View SolutionIf two angles and a side of one triangles are equal to two angles and a side of another triangles , the triangles are congruent.
View SolutionShow that the two triangles given the following figure are congruent.
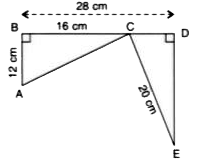
View SolutionWhich of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600 If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionIn the figure, the two triangles are congruent.The corresponding parts are marked. We can Write ΔRATE ?
View SolutionGiven below are measurements of some parts of two triangles. Examine whether the two triangles are congruent or not, by using SAS congruence rule. If the triangles are congruent, write them in symbolic form. ΔDEF
View SolutionGiven below are measurements of some parts of two triangles. Examinewhether the two triangles are congruent or not, using RHS congruencerule. In case of congruent triangles, write the result in symbolic form
View SolutionWhich of the following statements are true and which are false;
All squares are congruent.
If two squares have equal areas, they are congruent.
If two rectangles have equal areas, they are congruent.
If two triangles have equal areas, they are congruent.
View SolutionIf the length of two sides of an isosceles triangle are 3 and 7, what is the perimeter of the triangle?
View Solution
