Question

An aeroplane can carry a maximum of 200 passengers. A profit of Rs. 800 is made on each first class ticket and a profit of Rs. 500 is made on each second class ticket. The airline reserves at least 20 seats for first class. However, at least 4 times as many passengers prefer to travel by second class than by first class. Determine how many tickets of each type must be sold in order to maximize the profit of airline? Also find the maximum profit.

Explanation

Let number of Executive class air ticket sold be `x`
and number of Economy class air ticket sold be `y`

According to Question:

Maximum Seating Capacity is 200
`therefore` `x+y<=200 " " " " ....(1)`

Atleast 20 tickets are reserved for executive class
`therefore x>=20 " " " " ....(2)`

umber of tickets of economy class should be atleast 4 times the Executive class
`therefore y>=4x`
`y-4x>=0 " " " " ....(3)`

As, we need to maximize the profit, hence the function used is Maximize `Z`

Profit on executive class = Rs 1000
Profit on economy class = Rs 600

`therefore` Maximize `Z=1000x+600y`

Combining all constraints:

Max. `Z=1000x+600y`
`x+y<=200`
`x>=20`
`y-4x>=0 `
`x>=0,y>=0`




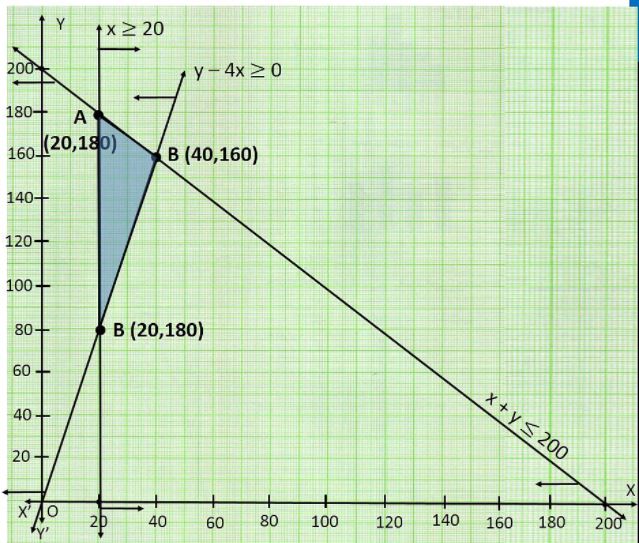
Hence, profit will be maximum, if

` " " " ` Tickets of executive class =40
` " " " ` Tickets of economy class =160
` " " " ` Maximum Profit = Rs 136000