A toy manufacturer produces two types of dolls; a basic version doll A and a deluxe version doll B. Each doll of type B takes twice as long to produce as one doll of type A. The company have time to make a maximum of 2000 dolls of type A per day, the supply of plastic is sufficient to produce 1500 dolls per day and each type requires equal amount of it. The deluxe version i.e. type B requires a fancy dress of which there are only 600 per day available. If the company makes a profit of RLs. 3 and Rs. 5 per doll, respectively, on doll A and B; how many of each should be produced per day in order to maximize profit? Solve it by graphical method.
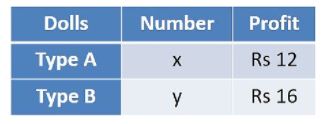
Let the number of dolls of type A be x
& the number of dolls of type B be y
According to Question,
Since combined production level should not exceed 1200 dolls
∴x+y≤1200 ...,(1)
Also, production level of dolls of type A exceeds 3 times the production of type B by atmost 600.
∴x−3y≤600 ...,(2)
And, demand of dolls of type is at most half of that of type A.
∴y≤x2
2y−x≤0 ....(3)
We need to maximize the profit
Here,
Profit on Type A dolls = Rs 12
Profit on Type B dolls = Rs 16
∴Z=12x+16y
Combining all constraints,
Maximize Z=12x+16y
x+y≤1200
x+y≤1200
2y−x≤0
x,y≥0

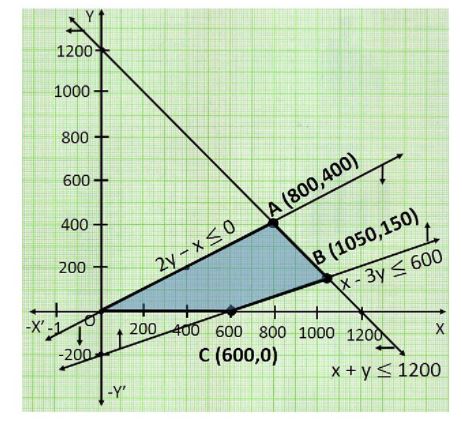
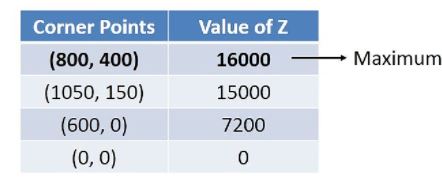
Hence, the profit will be maximum id, the company produces
Type A dolls=800
Type B dolls=400
& Max. Profit = Rs.16000
Topper's Solved these Questions
- BOOK - NCERT ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - SOLVED EXAMPLES11videos
LINEAR PROGRAMMING
- BOOK - NCERT ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXERCISE 12.211videos
LINEAR PROGRAMMING
- BOOK - NCERT ENGLISHCHAPTER - LINEAR PROGRAMMINGEXERCISE - EXERCISE 12.211videos
LINEAR PROGRAMMING
- BOOK - NCERT ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Solved Examples13videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - NCERT ENGLISHCHAPTER - MATRICESEXERCISE - All Questions105videos
MATRICES
Similar Questions
A toy company manufactures two types of doll; a basic version doll; a basic version doll A and a deluxe version doll B. Each doll of type B takes twice as long to produce as one of type. A and the company would have time to ,make a maximum of 2, 000 per day if it produces only the basic version. The supply of plastic is sufficient to produce 1500 dolls per day (both A and B combined). The deluxe version requires a fancy dress of which there are only 600 per day available. If the company makes profit Rs. 3 and Rs. 5 per doll respectively o doll A and doll B; how many of each should be produced per day in order to maximize profit?
View SolutionTwo types of flowers are produced by
View SolutionA firm manufactures two types of products, A and B, and sells them at a profil of 3 per unit to type B product and 5 perunit of type A product. Both product is processed on two machines M1and M2 One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2i whereas one unit of type B requires one minute of processing time on M1 and one minute on M Machines sells them at a profit of 5 per unit of type A and M, and M, are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product the firn should produce a day in order to maximize the profit. Solve the problem graphically [CHSE 2000]
View SolutionA company makes two kinds of leather belts, A and B. Belt A is high quality belt, and B is of lower quality. The respective profits are Rs. 40 and Rs. 30 per belt. Each belt of type A requires twice as much time as a belt of type B, and if all belts were of type B, the company could make 1000 belts per day. The supply of leather is sufficient for only 800 belts per day (both A and B combined). Belt A requires a fancy buckle, and only 400 buckles per day are available. There are only 700 buckles available for belt B. What should be the daily production of each type f belt? Formulate the problem as a LPP.
View SolutionThe types of waves produced in a sonometer wire are
View SolutionA manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the tune (in minutes) required for each toy on the machines is given below:
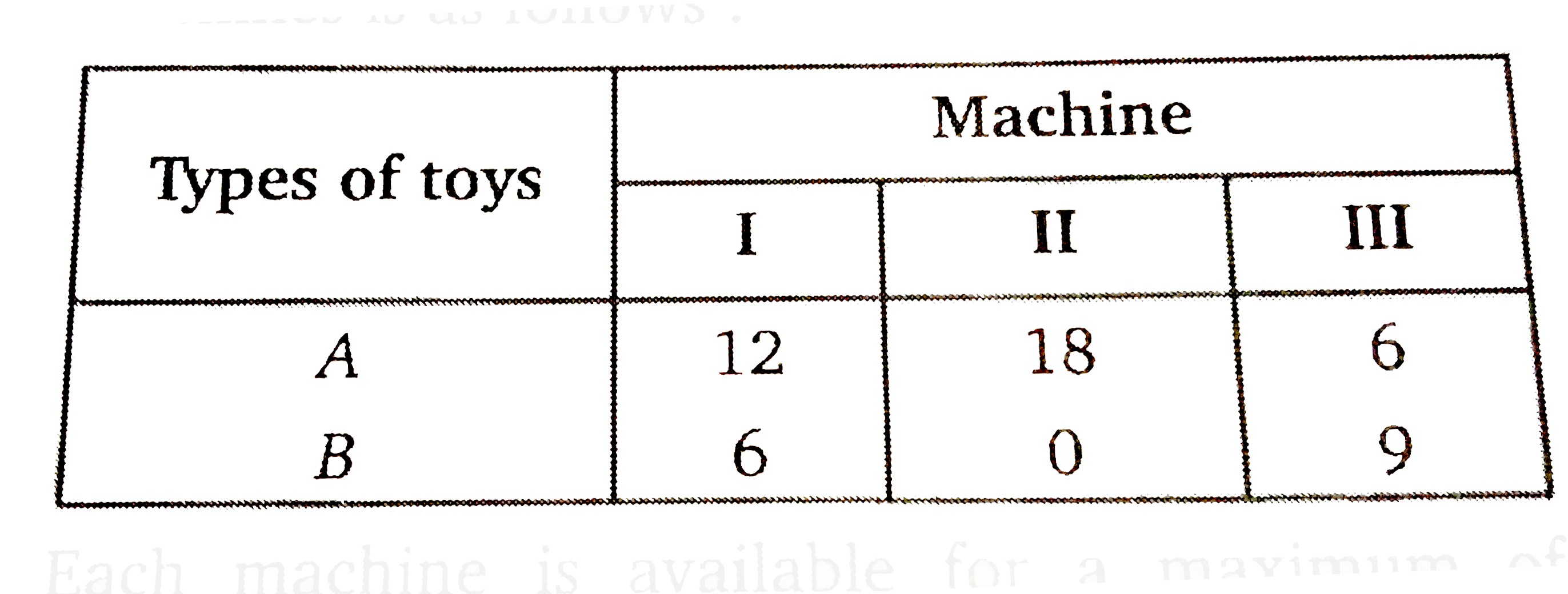 Each machine is available for a
maximum of 6 hours per day. If the profit View Solution
Each machine is available for a
maximum of 6 hours per day. If the profit View SolutionA small firm manufactures items A and B. The total number of items that it can manufacture in a day is at the most 24 Item A takes on hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be 300 and that on one unit of item B be 160, how many of each type of item should be produced to maximize the profit? Solve the problem graphically
View SolutionName two types of producers.
View SolutionA company produces two types of goods A and B, that require gold and silver. Each unit of type A requires 3 g of silver and 1 g of gold while that of type B requires 1 g of silver and 2 g of gold. The company can procure a maximum of 9 g of silver and 8 g of gold. If each unit of type A brings a profit of Rs 40 and that of type B Rs 50, formulate LPP to maximize profit.
View SolutionSaliva produced per day is
View Solution

