An ant is moving around a few food pieces of different shapes scattered on the floor. For which food-piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c=2πr, where r is the radius of the circle.
To solve the problem of determining which food piece the ant would have to take a longer round, we will calculate the perimeter (or circumference) of each food piece. Let's break it down step by step.
Step 1: Identify the Shapes and Given Dimensions
1. Shape A: A semicircle with a diameter of 2.8 cm.
2. Shape B: A semicircular top with a rectangular part (height 1.5 cm) and a diameter of 2.8 cm.
3. Shape C: A semicircular part with two straight lines (2 cm each) and a diameter of 2.8 cm.
Step 2: Calculate the Perimeter of Shape A
- Circumference of a full circle: C=2πr
- Radius: r=diameter2=2.82=1.4cm
- Circumference of the semicircle: C2=2πr2=πr=π×1.4
- Using π≈227:
Circumference of semicircle=227×1.4=22×1.47=30.87≈4.4cm
- Adding the diameter:
Total perimeter=4.4+2.8=7.2cm
Step 3: Calculate the Perimeter of Shape B
- Perimeter includes: the semicircular part and the two straight sides (1.5 cm each).
- Circumference of the semicircle:
Circumference of semicircle=πr=227×1.4≈4.4cm
- Total perimeter:
Total perimeter=4.4+1.5+1.5=4.4+3=7.4cm
Step 4: Calculate the Perimeter of Shape C
- Perimeter includes: the semicircular part and two straight lines (2 cm each).
- Circumference of the semicircle:
Circumference of semicircle=πr=227×1.4≈4.4cm
- Total perimeter:
Total perimeter=4.4+2+2=4.4+4=8.4cm
Step 5: Compare the Perimeters
- Perimeter of Shape A: 7.2 cm
- Perimeter of Shape B: 10.2 cm
- Perimeter of Shape C: 8.4 cm
Conclusion
The ant will have to take the longest round around Shape B, which has a perimeter of 10.2 cm.
---
1. Shape A: A semicircle with a diameter of 2.8 cm.
2. Shape B: A semicircular top with a rectangular part (height 1.5 cm) and a diameter of 2.8 cm.
3. Shape C: A semicircular part with two straight lines (2 cm each) and a diameter of 2.8 cm.
- Circumference of a full circle: C=2πr
- Radius: r=diameter2=2.82=1.4cm
- Circumference of the semicircle: C2=2πr2=πr=π×1.4
- Using π≈227:
Circumference of semicircle=227×1.4=22×1.47=30.87≈4.4cm
- Adding the diameter:
Total perimeter=4.4+2.8=7.2cm
- Perimeter includes: the semicircular part and the two straight sides (1.5 cm each).
- Circumference of the semicircle:
Circumference of semicircle=πr=227×1.4≈4.4cm
- Total perimeter:
Total perimeter=4.4+1.5+1.5=4.4+3=7.4cm
- Perimeter includes: the semicircular part and two straight lines (2 cm each).
- Circumference of the semicircle:
Circumference of semicircle=πr=227×1.4≈4.4cm
- Total perimeter:
Total perimeter=4.4+2+2=4.4+4=8.4cm
- Perimeter of Shape A: 7.2 cm
- Perimeter of Shape B: 10.2 cm
- Perimeter of Shape C: 8.4 cm
The ant will have to take the longest round around Shape B, which has a perimeter of 10.2 cm.
Topper's Solved these Questions
- BOOK - RD SHARMA ENGLISHCHAPTER - LINEAR EQUATION IN ONE VARIABLEEXERCISE - All Questions110videos
LINEAR EQUATION IN ONE VARIABLE
- BOOK - RD SHARMA ENGLISHCHAPTER - MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)EXERCISE - All Questions134videos
MENSURATION-II (VOLUMES AND SURFACE AREAS OF A CUBOID AND A CUBE)
Similar Questions
The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.

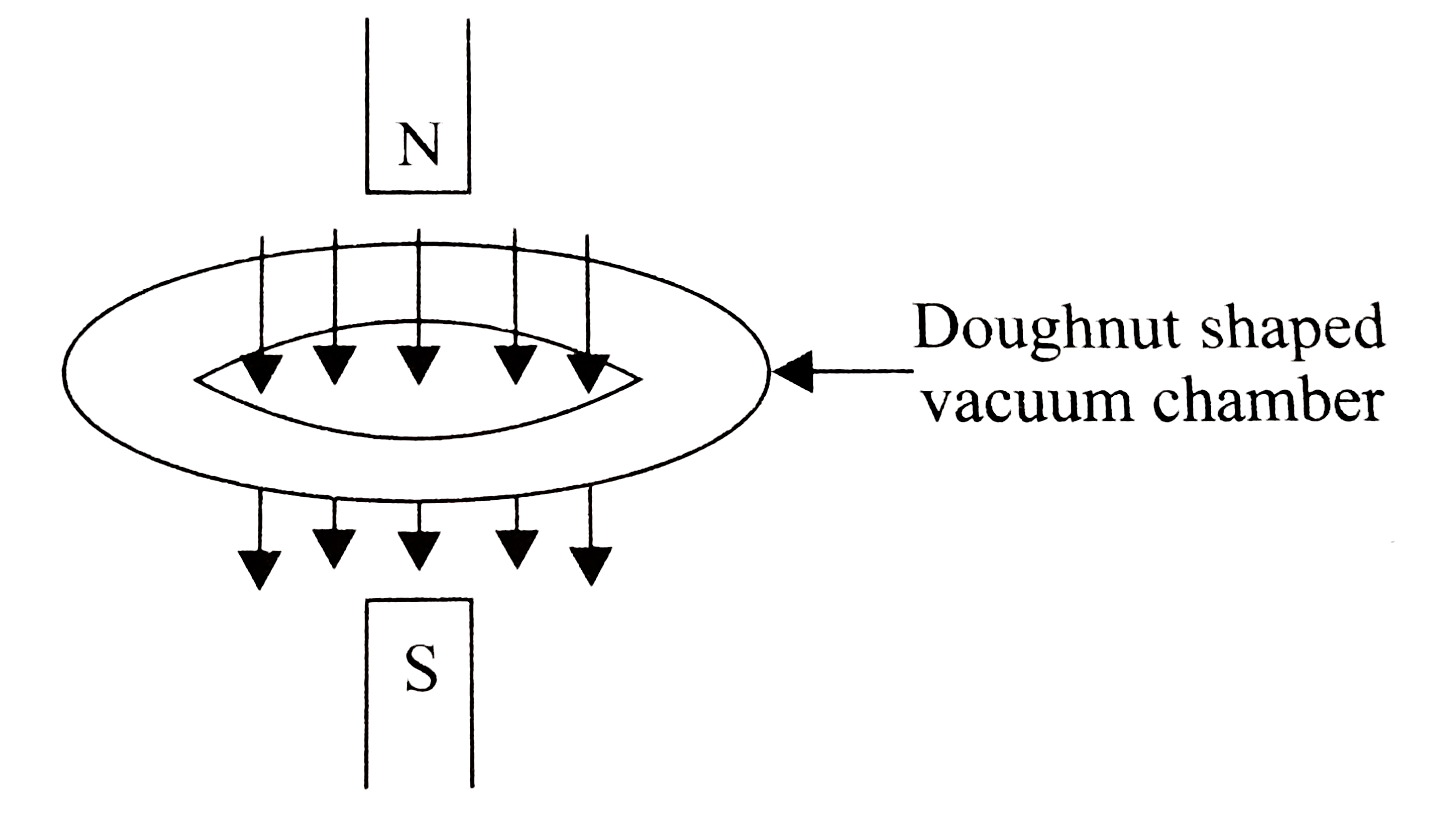
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Variable magnetic fluxView SolutionThe fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Magnetic field which keeps the particles in circular path mustView Solution
Knowledge Check
- Question 1 - Select One
Uniform cicular motion is used in physics to describe the motion of an object traveling at a constant speed in a circle. The speed of the object is called tangential velocity and it can be calculated using the formula abovce, where r is the radius of the circle and T is the time is takes for the object to make one complete circle, called a peroid. WHich of the following formulas could be used to find the length of one period if you know the tengential velocity and the radius of the circle ?
AT=v2πrBT=2πrvCT=2πrvDT=12πrv
The fact tht a changing magnetic flux produces an electric field is basic to the operation of many high energy particle accelerators. Since the principle was first successfully applied to the acceleration of electrons (or beta particles) in a device called the betatron, this method of acceleration is often given that name. The general idea involved is shown in Fig.
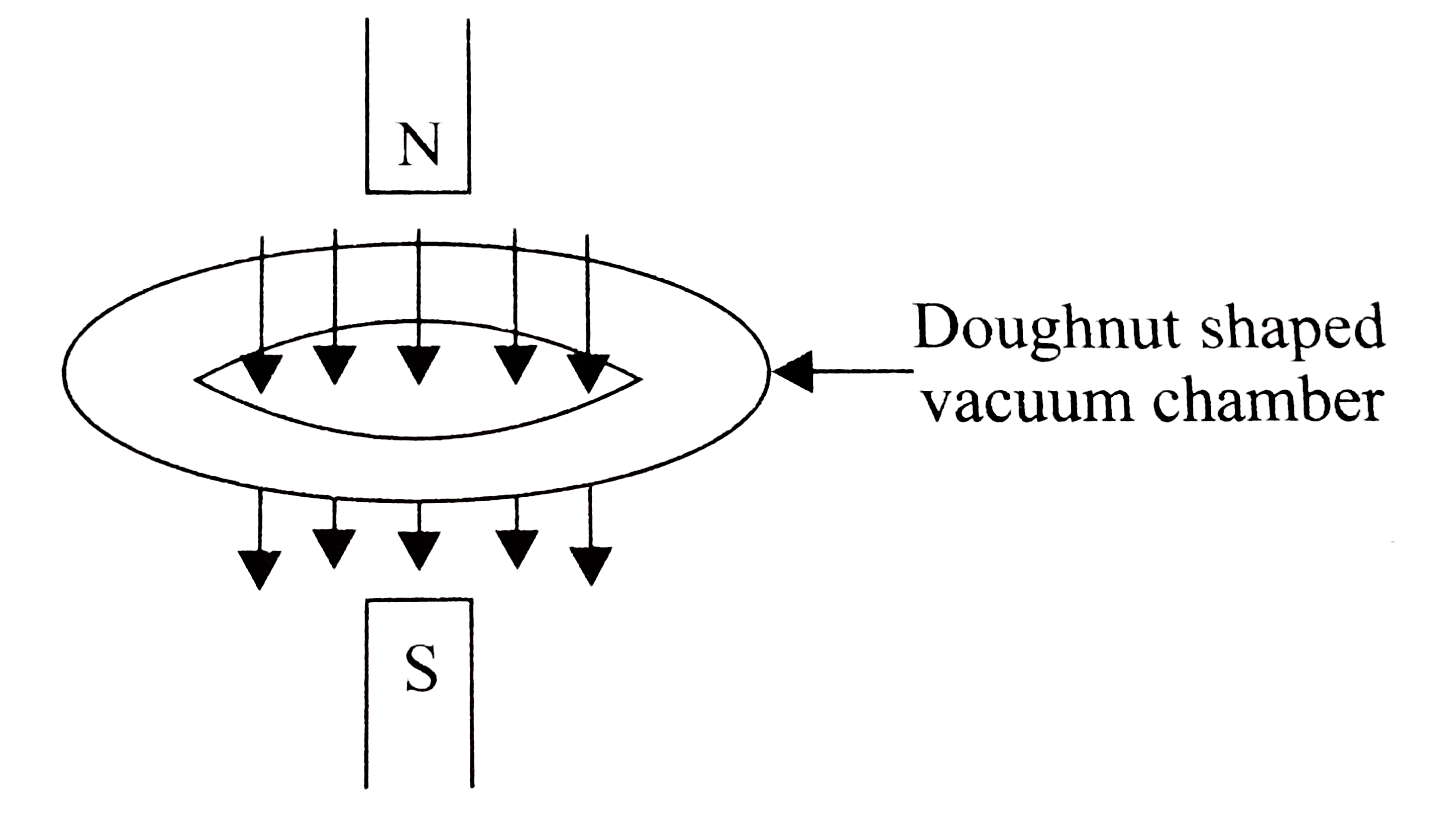
An electromagnet is used to produce a changing flux through a circular loop defined by the doughnut shaped vacuum chamber. We see that there will be an electric field E along the circular length of the doughnut, i.e. circling the magnet poles, given by 2πaE=d(ϕ)/dt, where 'a' is the radius of the doughnut. Any charged particle inside the vacuum chamber will experience a force qE and will accelerate. Ordinarily, the charged particle would shoot out the vacuum chamber and becomes lost.
However, if the magnetic field at the position of the doughnut is just proper to satisfy the relation,
Centripetal force = magnetic force or mv2/a=qvB then the charge will travel in a circle within the doughnut. By proper shaping of the magnet pole piece, this relation can be satisfied. As a result, the charge will move at high speed along the loop within the doughnut. Each time it goes around the loop, it has, in effect, fallen through a potential difference equal to the induced emf, namely ε=(d(ϕ)/dt). Its energy after 'n' trips around the loop will be q(n(ε)).
Working of betatron is not based upon which of the following theories?View SolutionLet C1,C2,,Cn be a sequence of concentric circle. The nth circle has the radius n and it has n openings. A points P starts travelling on the smallest circle C1 and leaves it at an opening along the normal at the point of opening to reach the next circle C2 . Then it moves on the second circle C2 and leaves it likewise to reach the third circle C3 and so on. Find the total number of different path in which the point can come out of nth circle.
View SolutionConsider a vertical tube open at both ends. The tube consistss of two parts, each of different cross sections and each part having a piston which can move smoothly in respective tubes. The two piston which can move smoothly in respective tube wire. The piston are joined together by an inextensible wire. The combined mass of the two piston is 5kgand area of cross section of the upper piston is 10cm2 greater than that of the lower piston. Amount of gas enclosed by the pistons is 1mol. When the gas is heated slowly, pistons move by 50cm. Find the rise in the temperature of the gas in the form X/RK, where R is universal gas constant. Use g=10m/s2 and outside pressure =105N/m2).
 View Solution
View SolutionConsider a vertical tube open at both ends. The tube consistss of two parts, each of different cross sections and each part having a piston which can move smoothly in respective tubes. The two piston which can move smoothly in respective tube wire. The piston are joined together by an inextensible wire. The combined mass of the two piston is 5kgand area of cross section of the upper piston is 10cm2 greater than that of the lower piston. Amount of gas enclosed by the pistons is 1mol. When the gas is heated slowly, pistons move by 50cm. Find the rise in the temperature of the gas in the form X/RK, where R is universal gas constant. Use g=10m/s2 and outside pressure =105N/m2).
 View Solution
View SolutionWeight of a body depends directly upon acceleration due to gravity g. Value of g depends upon many factors. It depends upon the shape of earth, rotation earth etc. Weight of a body at a pole is more then that at a place on equator because g is maximum at poles and minimum on equator. Acceleration due to gravity g varies with latitude λ as per relation given below :
grot=g−Rω2cos2λ where R is radius of earth and ω is angular velocity of earth. A body of mass m weighs Wr in a train at rest. The train then begins to run with a velocity v around the equator from west to east. It observed that weight Wm of the same body in the moving train is different from Wr. Let vebe the velocity of a point on equator with respect to axis of rotation of earth and R be the radius of the earth. Clearly the relative between earth and trainwill affect the weight of the body.
Difference between Weight Wr and the gravitational attraction on the body can be given asView SolutionWeight of a body depends directly upon acceleration due to gravity g. Value of g depends upon many factors. It depends upon the shape of earth, rotation earth etc. Weight of a body at a pole is more then that at a place on equator because g is maximum at poles and minimum on equator. Acceleration due to gravity g varies with latitude λ as per relation given below :
grot=g−Rω2cos2λ where R is radius of earth and ω is angular velocity of earth. A body of mass m weighs Wr in a train at rest. The train then begins to run with a velocity v around the equator from west to east. It observed that weight Wm of the same body in the moving train is different from Wr. Let vebe the velocity of a point on equator with respect to axis of rotation of earth and R be the radius of the earth. Clearly the relative between earth and trainwill affect the weight of the body.
Weight Wm of the body can be given asView SolutionDirection :
Resistive force proportional to object velocity
At low speeds, the resistive force acting on an object that is moving a viscous medium is effectively modeleld as being proportional to the object velocity. The mathematical representation of the resistive force can be expressed as
R=−bv
Where v is the velocity of the object and b is a positive constant that depends onthe properties of the medium and on the shape and dimensions of the object. The negative sign represents the fact that the resistance froce is opposite to the velocity.
Consider a sphere of mass m released frm rest in a liquid. Assuming that the only forces acting on the spheres are the resistive froce R and the weight mg, we can describe its motion using Newton's second law. though the buoyant force is also acting on the submerged object the force is constant and effect of this force be modeled by changing the apparent weight of the sphere by a constant froce, so we can ignore it here.
Thus mg−bv=mdvdt⇒dvdt=g−bmv
Solving the equation
v=mgb(1−e−bt/m)
where e=2.71 is the base of the natural logarithm
The acceleration becomes zero when the increasing resistive force eventually the weight. At this point, the object reaches its terminals speed v1 and then on it continues to move with zero acceleration
mg−bT=0
⇒mT=mgb
Hence v=vT(1−evtm)
In an experimental set-up four objects I,II,III,IV were released in same liquid. Using the data collected for the subsequent motions value of constant b were calculated. Respective data are shown in table.
ObjectIIIIIIVMass (in kg.)1234Constant bin (N-s)/m3.71.41.42.8
If buoyant force were also taken into account then value of terminal speed would haveView Solution

