An ice-ceram cone full of ice-cream having radius 5 cm height 10 cm as shown if figure.
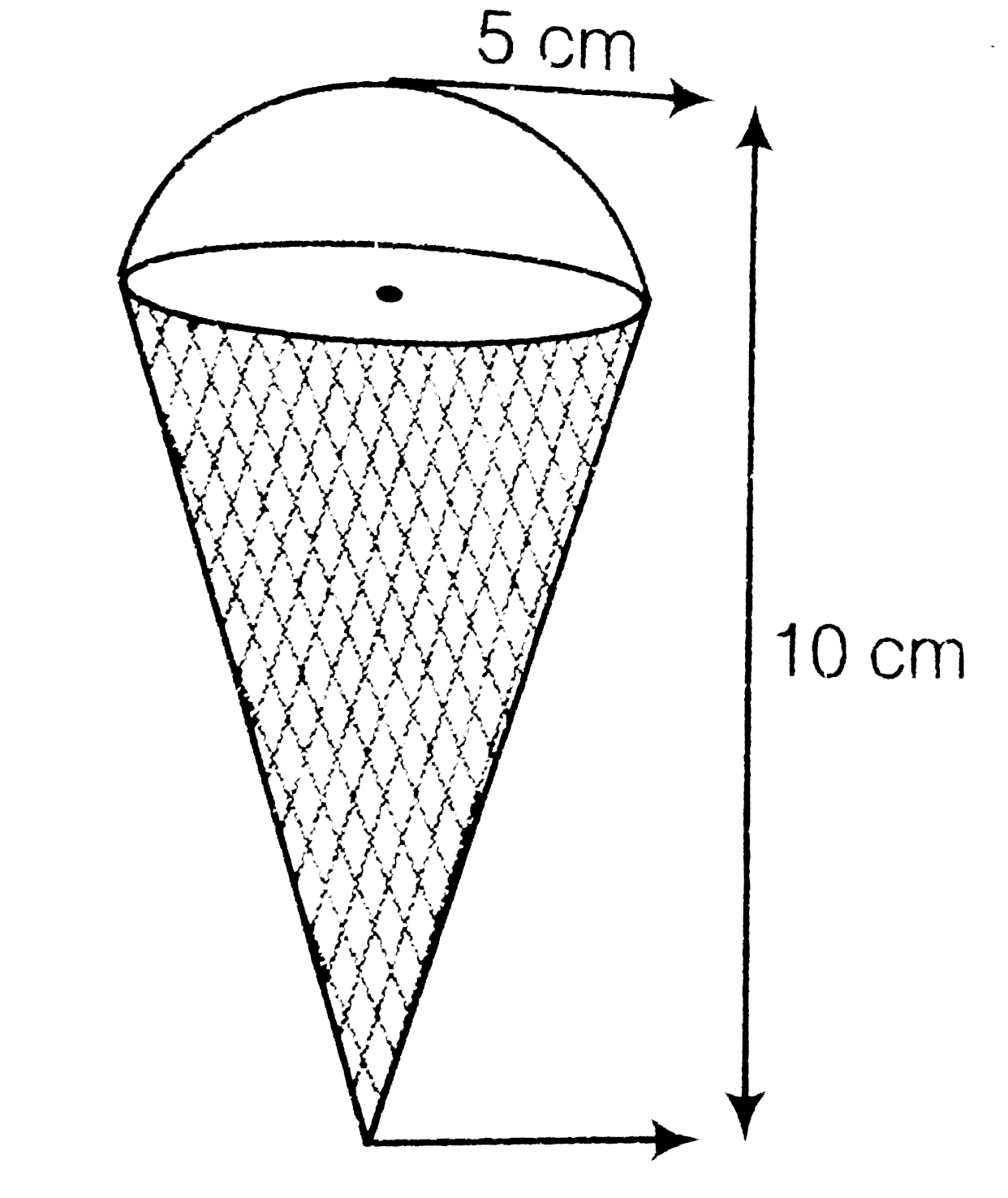
Calculate the volume of ice-cream, provided that its 16 part is left unfilled with ice-cream.
Given , ice - cream cone is the combination of a hemisphere and a cone.
Also, radius of hemisphere = 5 cm
∴ Volume of hemisphere =23πr3=23×227×(5)3
=550021=261.90cm3
Now, radius of the cone = 5 cm
and heigth of the cone = 10-5 = cm
∴ Volume of the cone =13πr2h
=13×227×(5)2×5
=275021=130.95cm3
Now, total volume of ice- cream cone=261.90+130.95=392.85cm3
Since,16 parts is left unfilled with ice- cream.
∴ Required volume of ice - cream =392.85−392.85×16=392.85−64.475
=327.4cm3
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - LONG ANSWER TYPE QUESTIONS20videos
SURFACE AREAS AND VOLUMES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS8videos
SURFACE AREAS AND VOLUMES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - STATISTICS AND PROBABILITYEXERCISE - LONG ASWERS QUESTIONS14videos
STATISTICS AND PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - TRIANGLESEXERCISE - Long Answer Type Questions18videos
TRIANGLES
Similar Questions
A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream. The ice-cream is to be filled in cones of height 12 cm and diameter 6 cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA right circular cylinder having diameter 12cm and height 15cm is full of ice-cream. The ice-cream is to be filled in cones of height 12cm and diameter 6cm having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream.
View SolutionA container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
View SolutionThe given figure shows the cross-section of an ice cream cone consisting of a cone surmounted by a hemisphere. The radius of the hemisphere is 3.5 cm and the height of the cone is 10-5 cm. The outer shell ABCDEF is shaded and is not filled with ice-cream. AF = DC = 0.5 cm, AB // FE and BC // ED. Calculate :
(i) the volume of the ice-cream in the cone (the internal volume of the cone including the hemisphere) in cm3,
(ii) the volume of the outer shell (the shaded portion) in cm3.
In each case, give your answer correct to the nearest cm3.
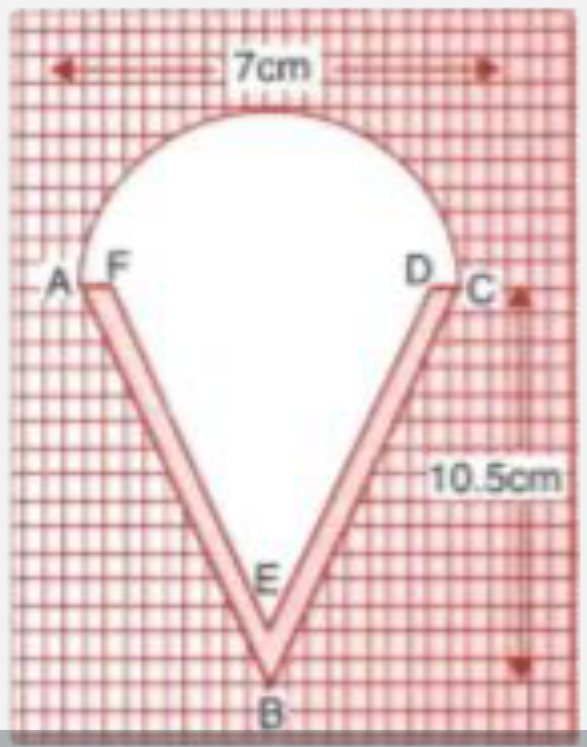 View Solution
View SolutionA cylindrical vessel with internal diameter 10 cm and height 10.5 cm is full of water. A solid cone of base diameter 7 cm and height 6 cm is completely immersed in water. Find the volume of water (i) displaced out of the cylinder (ii) left in the cylinder. (Take π=22/7 )
View SolutionA cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is four times the radius of its base, find the radius of the ice-cream cone.
View SolutionA cylindrical container of radius 6 cm and height 15 cm is filled with ice-cream. The whole ice-cream has to be distributed to 10 children in equal cones with hemispherical tops. If the height of the conical portion is four times the radius of its base, find the radius of the ice-cream cone.
View SolutionA cylindrical container is filled with ice-cream, whose diameter is 12 cm and height is 15 cm. The whole ice-cream is distributed to 10 children in equal cones having hemispherical tops. If the height of the conical portion is twice the diameter of its base, find the diameter of the ice-cream.
View SolutionShown in the figure is a hollow ice-cream cone (it is open at the top). If its mass is M, radius of its top , R and height , H, then its moment of inertia its axis is :
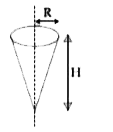 View Solution
View Solution

