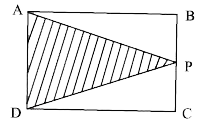
Area of parallelogram ABCD (Fig. 9.16) is not equal to

DEX DC
BE X AD
BF X DC
BEX BC
Step by step video & image solution for Area of parallelogram ABCD (Fig. 9.16) is not equal to by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Exercise (Fill in the blanks)19videos
PERIMETER AND AREA
- BOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Exercise (True or false)7videos
PERIMETER AND AREA
- BOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Think and Discuss7videos
PERIMETER AND AREA
- BOOK - NCERT EXEMPLARCHAPTER - LINES AND ANGLES EXERCISE - Exercise (fill in the blanks)3videos
LINES AND ANGLES
- BOOK - NCERT EXEMPLARCHAPTER - PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESEXERCISE - EXERCISE108videos
PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPES
Similar Questions
Knowledge Check
- Question 1 - Select One
The area of a parallelogram ABCD is equal to that right angled isosceles triangle whose hypotenuse is l cm. If O is a point inside the parallelogram ABCD then sum of areas of ΔAOBandΔCOD is.
Al22cm2Bl24cm2Cl28cm2Dl216cm2 - Question 2 - Select One
ABCD is a parallelogram P and R are two points on AB such that the area of parallelogram ABCD is 8 times the area of Δ DPR. If PR = 5 cm, then CD is equal to
A10 cmB5 cmC20 cmD12 cm
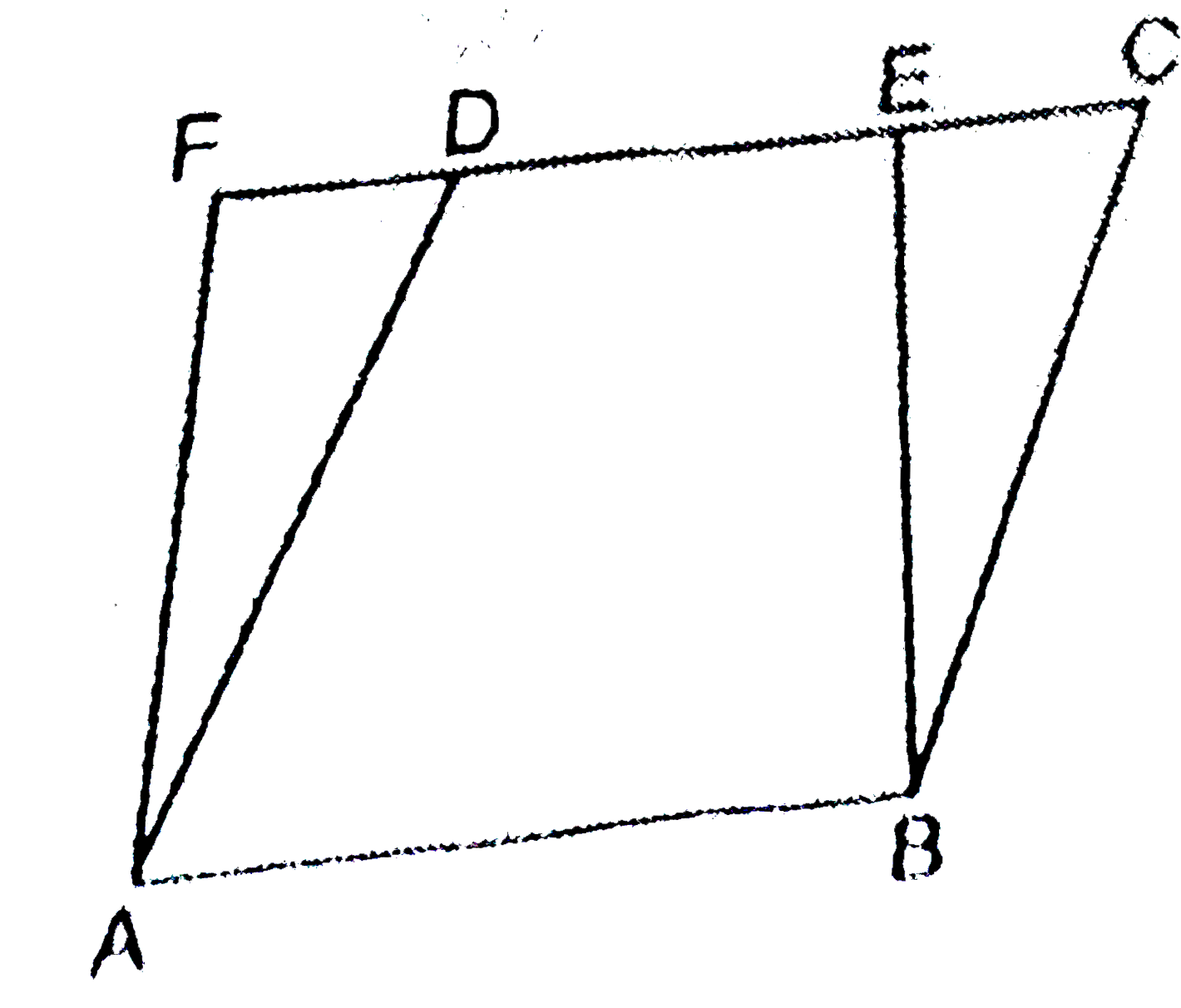
In the given figure, if the area of parallelogram ABCD is 40cm2, find the area of parallelogram ABEF
 View Solution
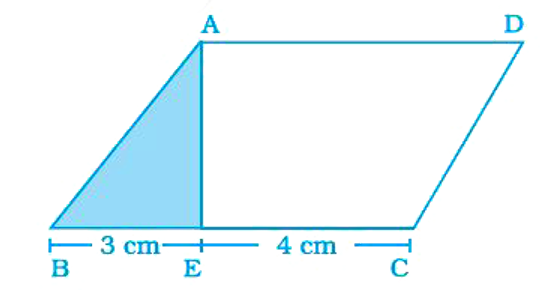
View SolutionIn Fig. 9.35, find the area of parallelogram ABCD if the area of shaded triangle is 9cm2.
 View Solution
View SolutionA(6,1),B(8,2) and C(9,4) are the vertices of a parallelogram ABCD. If E is the midpoint of DC, find the area of Δ ADE.
View SolutionABCD and BCFE are parallelgorams. If area of triangle EBC=480cm2,AB=30cmandBC=40cm. Calculate
(i) area of parallelogram ABCD
(ii) area of parallelogram BCEF
(iii) length of altitude from A on CD.
(iv) area of ΔECF
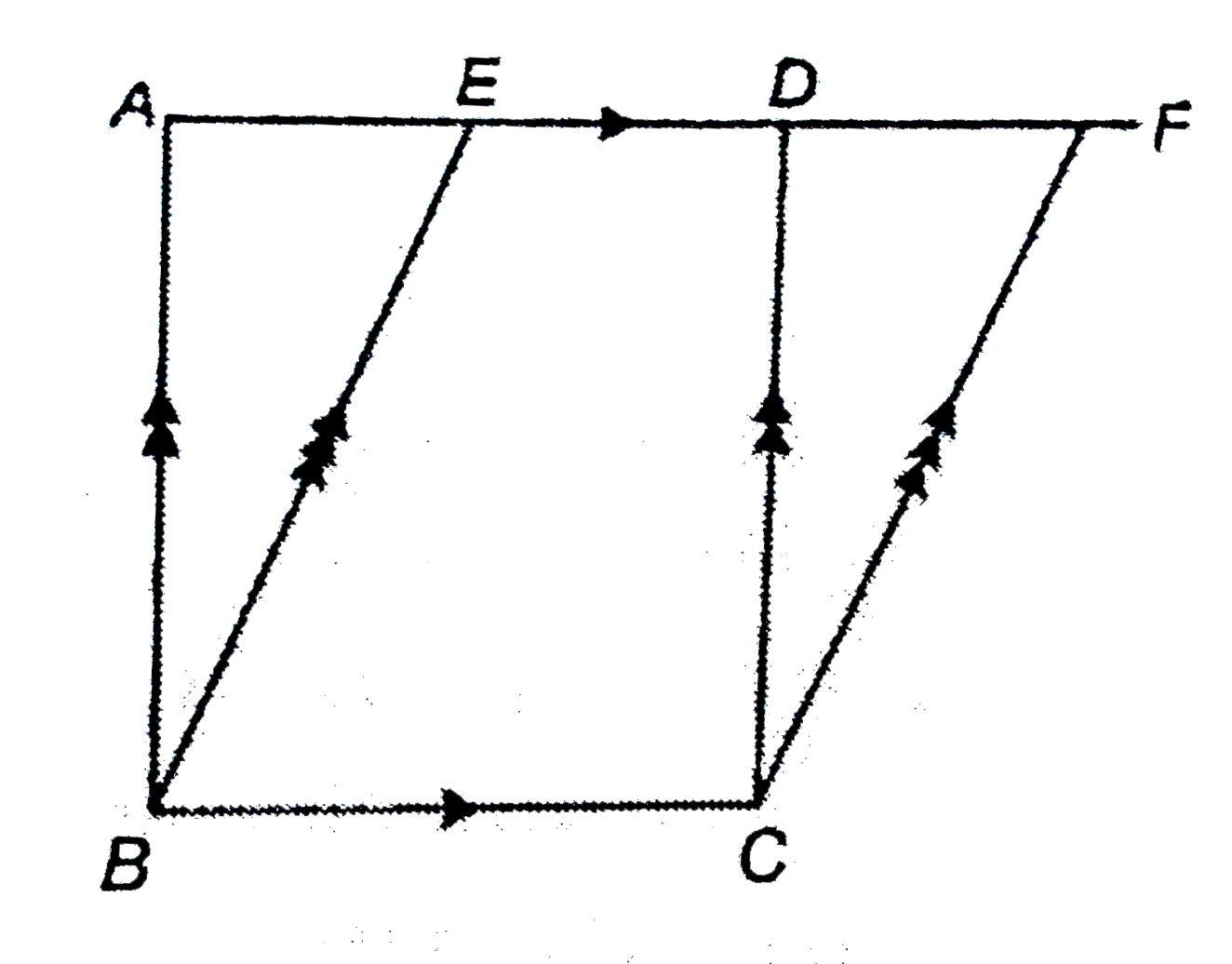 View Solution
View SolutionThe area of any parallelogram ABCD, is AB X BC.
View SolutionIn Fig. 9.32, area of ΔAFB is equal to the area of parallelogram ABCD. If altitude EF is 16 cm long, find the altitude of the parallelogram to the base AB of length 10 cm. What is the area of ΔDAO, where O is the mid point of DC?
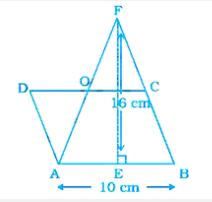 View Solution
View Solution