Calculate the area under the curve y=2√x included between the lines x = 0 and x = 1.
The correct Answer is:N/a
To calculate the area under the curve y=2√x between the lines x=0 and x=1, we will follow these steps:
Step 1: Set up the integral
The area A under the curve from x=0 to x=1 can be expressed as:
A=∫10(2√x)dx
Step 2: Simplify the integrand
We can rewrite 2√x as 2x1/2:
A=∫102x1/2dx
Step 3: Integrate the function
Using the power rule for integration, we have:
∫xndx=xn+1n+1+C
For our case, n=12:
∫2x1/2dx=2⋅x3/23/2=43x3/2
Step 4: Evaluate the definite integral
Now we evaluate this from 0 to 1:
A=(43x3/2)10=43(13/2)−43(03/2)
Calculating this gives:
A=43(1)−43(0)=43−0=43
Final Answer
Thus, the area under the curve y=2√x from x=0 to x=1 is:
43 square units
The area A under the curve from x=0 to x=1 can be expressed as:
A=∫10(2√x)dx
We can rewrite 2√x as 2x1/2:
A=∫102x1/2dx
Using the power rule for integration, we have:
∫xndx=xn+1n+1+C
For our case, n=12:
∫2x1/2dx=2⋅x3/23/2=43x3/2
Now we evaluate this from 0 to 1:
A=(43x3/2)10=43(13/2)−43(03/2)
Calculating this gives:
A=43(1)−43(0)=43−0=43
Thus, the area under the curve y=2√x from x=0 to x=1 is:
43 square units
Topper's Solved these Questions
- APPLICATION OF INTEGRALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Long Answer Type Questions
16 Videos
- APPLICATION OF INTEGRALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Objective Type Questions
22 Videos
- APPLICATION OF DERIVATIVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Fillers
5 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - True/False
10 Videos
Similar Questions
Determine the area under the curve y=√a2−x2 included between the lines x =0 and x = a.
View SolutionDetermine the area under the curve y=√a2−x2 included between the lines x=0andx=a.
View SolutionCalculate the area enclosed under the curve f(x)=x2 between the limits x=2 and x=3 (figure)
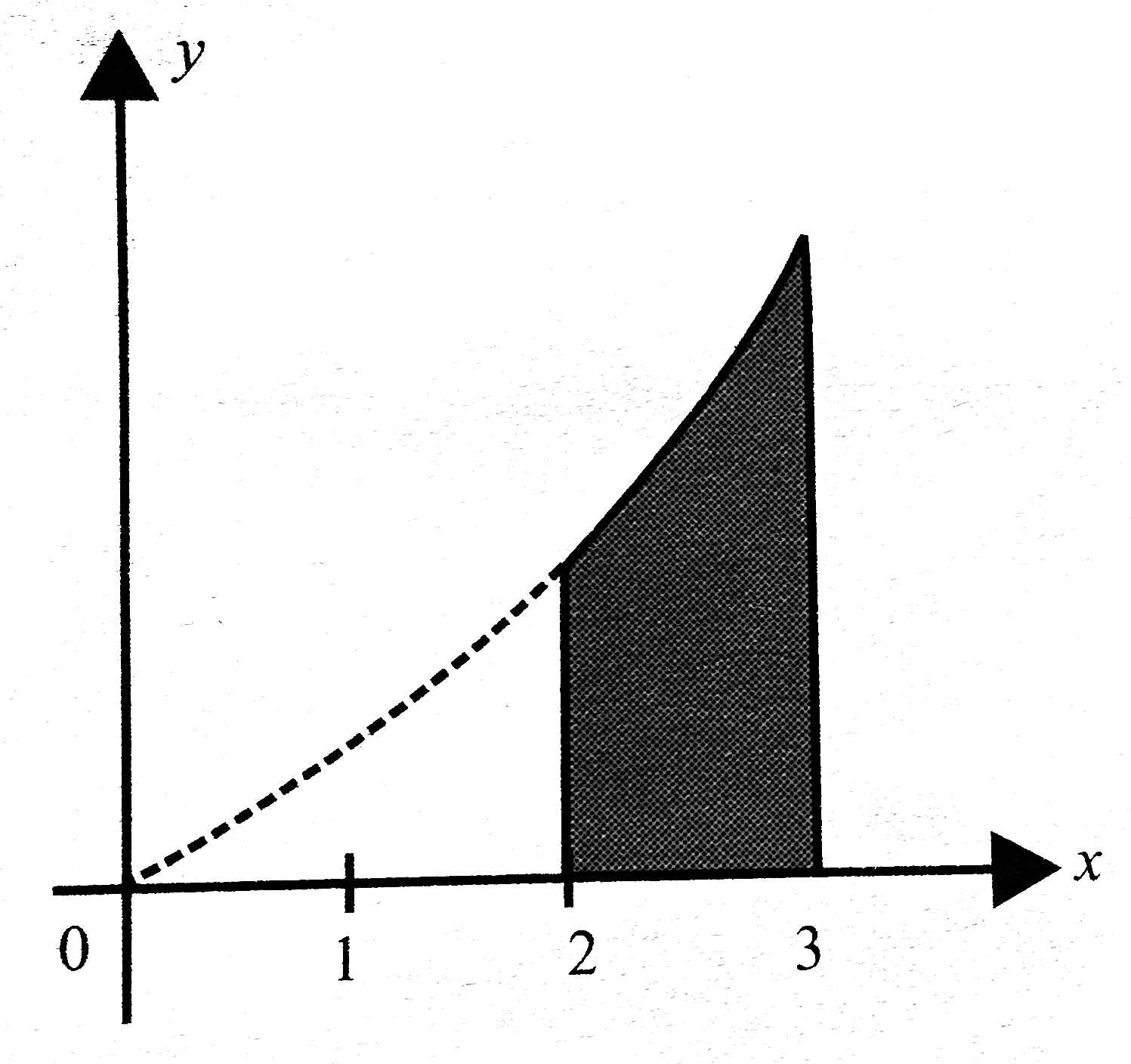
View SolutionDraw a rough sketch of the curve y=√x−1 in the interval [1, 5] and find the area under the given curve and between the lines x = 1 and x = 5.
View SolutionFind the area under the curve y=(x2+2)2+2x between the ordinates x =0 and x=2
View SolutionFind the area under the curve y=sin2x+cos2x between the ordinates x = 0, x=π4
View SolutionFind the area of the region bounded by the curves y=√x+2andy=1x+1 between the lines x=0 and x=2.
View SolutionFind the area included between the line y=x and the parabola x2=4y.
View SolutionThe area bounded by the curves y=cosx and y=sinx between the ordinates x=0 and x=3π2 is
View SolutionSketch the graph of y=|x+3| and evaluate the area under the curve y=|x+3| above x-axis and between x=6 to x=0.
View Solution
