CD and GH are respectively the bisectors of ∠ACBand ∠EGFsuch that D and H lie on sides AB and FE of ΔABC and ΔEFGrespectively. IfΔABCΔFEG, show that:(i) CDGH=AGFG (ii) DeltaD
Step by step video & image solution for CD and GH are respectively the bisectors of /_A C Band /_E G Fsuch that D and H lie on sides AB and FE of DeltaA B C\ and\ DeltaE F Grespectively. IfDeltaA B C DeltaF E G, show that:(i) (C D)/(G H)=(A G)/(F G) (ii) DeltaD by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SELF ASSESSMENT TEST
10 Videos
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - PROFICIENCY EXERCISE (SHORT ANSWER TYPE QUESTIONS-II)
39 Videos
- REAL NUMBERSBOOK - VK GLOBAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self -Assessment Test
11 Videos
- VALUE-BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-VII : (Statistics & Probability)
8 Videos
Similar Questions
In Fig. 4.103, CD and GH are respectively the medians of ABC and EFG . If ABC~FEG , prove that (FIGURE) ADC~FHG (ii) CDGH=ABFE (iii) CDB~GHE
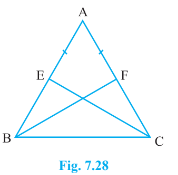
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionIn Fig. 4.102 (i) and (ii) , if CD and GH (D and H lie on AB and FE ) are respectively bisectors of ∠ACB and ∠EGF and ABC~FEG , prove that (FIGURE) DCA~HGF (ii) CDGH=ACFG (iii) DCB~HGE
View Solution
Identify A, B, C, D, E, F,G
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

View SolutionABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionD and E are points on sides AB and AC respectively of ΔABCsuch thatar (DBC) = ar (EBC). Prove that DE ∣∣ BC.
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View SolutionIn figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.

View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View Solution
