In fig.7.84, DEFG is a square and . Prove that:
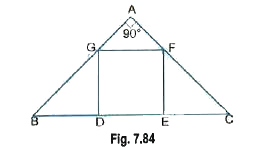
(i) (ii) (iii) (iv)
Step by step video & image solution for In fig.7.84, DEFG is a square and angleBAC = 90°. Prove that: <bR> <Br> (i) DeltaAGF~DeltaDBG (ii) DeltaAGF~ DeltaEFC (iii) DeltaDBG~ DeltaEFC (iv) DE^(2) = BD xx EC by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - SELF ASSESSMENT TEST
10 Videos
- TRIANGLESBOOK - VK GLOBAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - PROFICIENCY EXERCISE (SHORT ANSWER TYPE QUESTIONS-II)
39 Videos
- REAL NUMBERSBOOK - VK GLOBAL PUBLICATIONCHAPTER - REAL NUMBERSEXERCISE - Self -Assessment Test
11 Videos
- VALUE-BASED QUESTIONSBOOK - VK GLOBAL PUBLICATIONCHAPTER - VALUE-BASED QUESTIONSEXERCISE - Unit-VII : (Statistics & Probability)
8 Videos
Similar Questions
In the given figure, DEFG is a square and ∠BAC=90∘, Prove that
(i)ΔAGF~ΔDBG
(ii) ΔAGF~ΔEFC
(iii)DE2=BD×EC
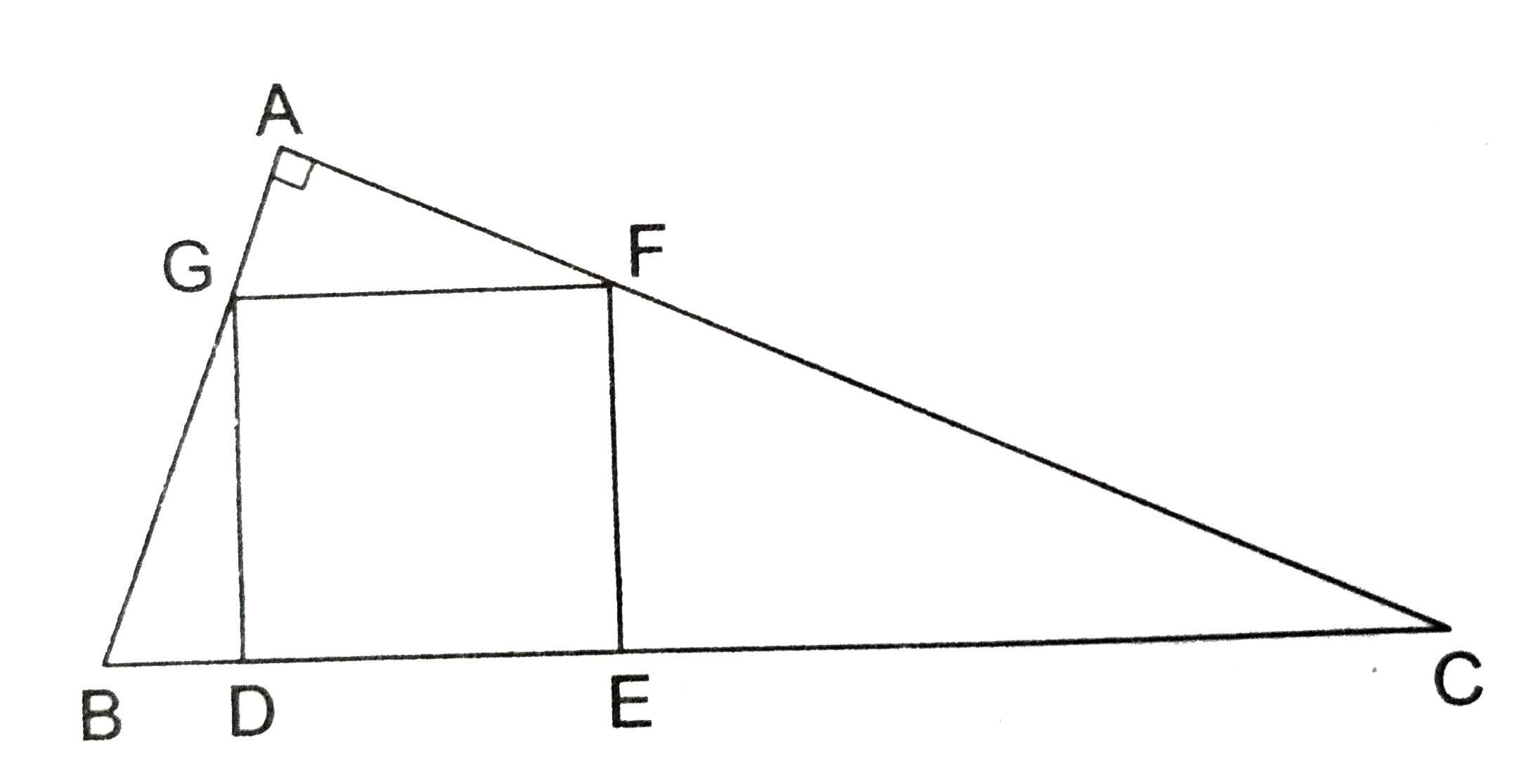
View SolutionIn the given figure , DEFG is a square and ∠BAC=90∘ prove that (i) △AGF~△DBG (ii)△AGF~△EFC
View SolutionIn the given figure DEFG is a square and ∠BAC=90∘ . Show that FG2=BG×FC .
View SolutionIn Fig. 4.128, DEFG is a square and ∠BAC=90o . Prove that AGFDBG (ii) AGFEFC (FIGURE) (iii) DBGEFC (iv) DE2=BD×EC
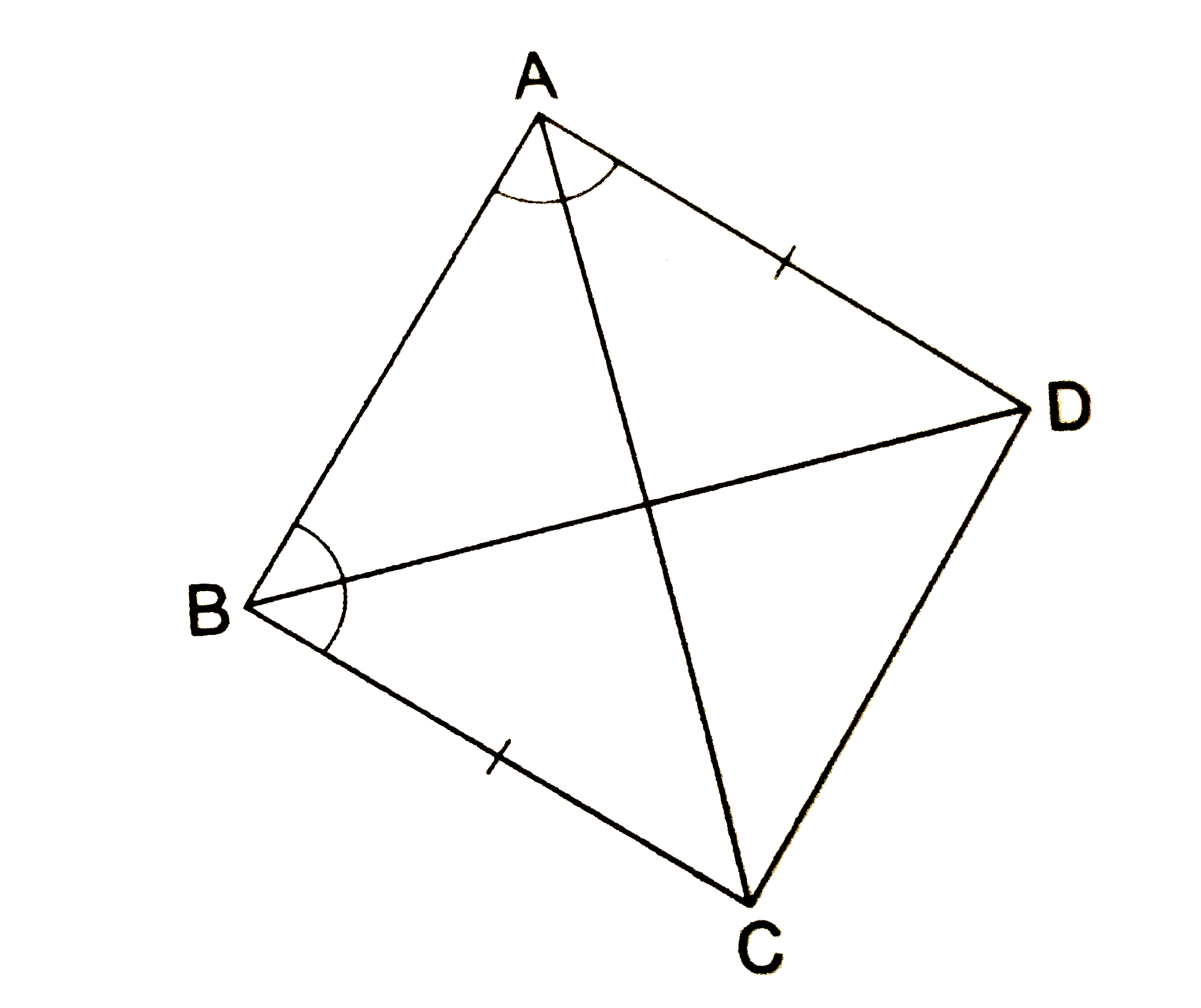
View SolutionIn the given figure, ABCD is a quadrilateral in which AD = BC and ∠DAB=∠CBA.
Prove that (i) ΔABD≅ΔBAC,
(ii) BD = AC,
(iii) ∠ABD=∠BAC.
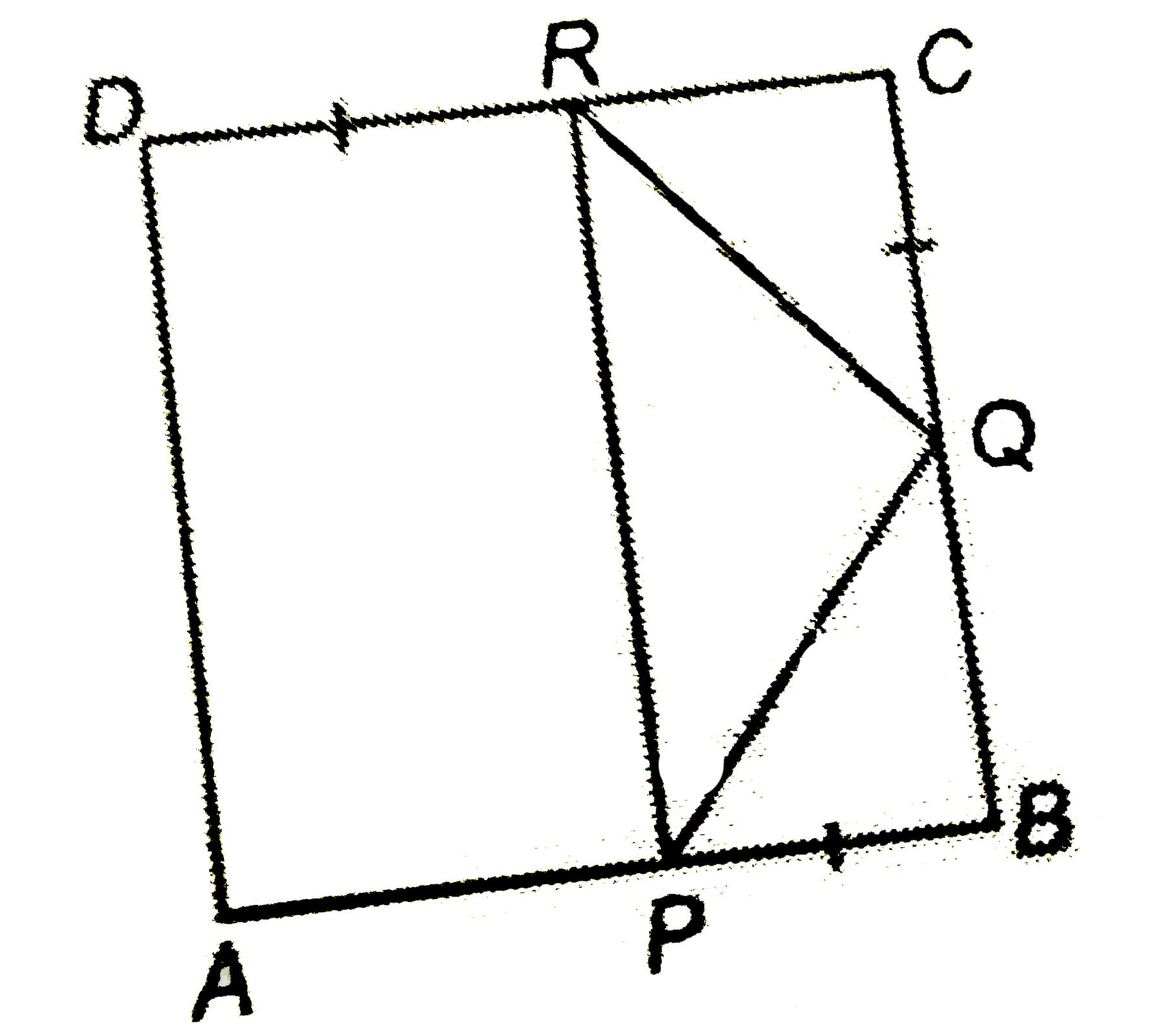
View SolutionIn the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘
View SolutionIn the given figure if ∠B=90∘ and BD is perpendicular to AC then
prove that:
(i)△ADB~△BDC(ii)△ADB~△ABC
(iii) △BDC~△ABC(iv)BD2=AD×DC
(v) AB2=AD×AC(vi)BC2=CD×AC
(vii) AB2+BC2=AC2

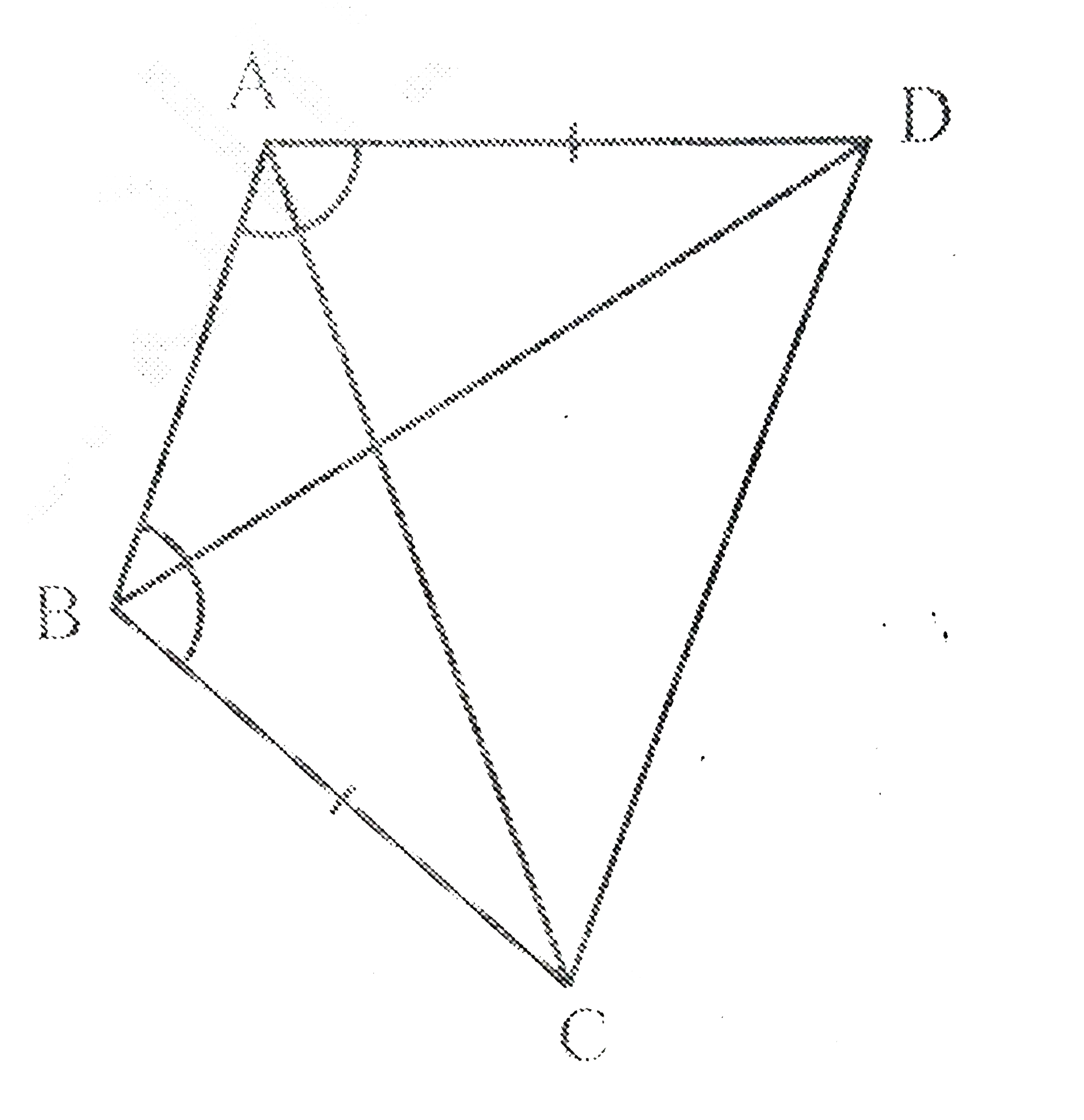
View SolutionABCD is a quadrilateral in which and∠DAB =∠CBA(see Fig. 7.17). Prove that
(i) ΔABD≅ΔBAC
(ii) BD = AC
(iii) ∠ABD =∠BAC
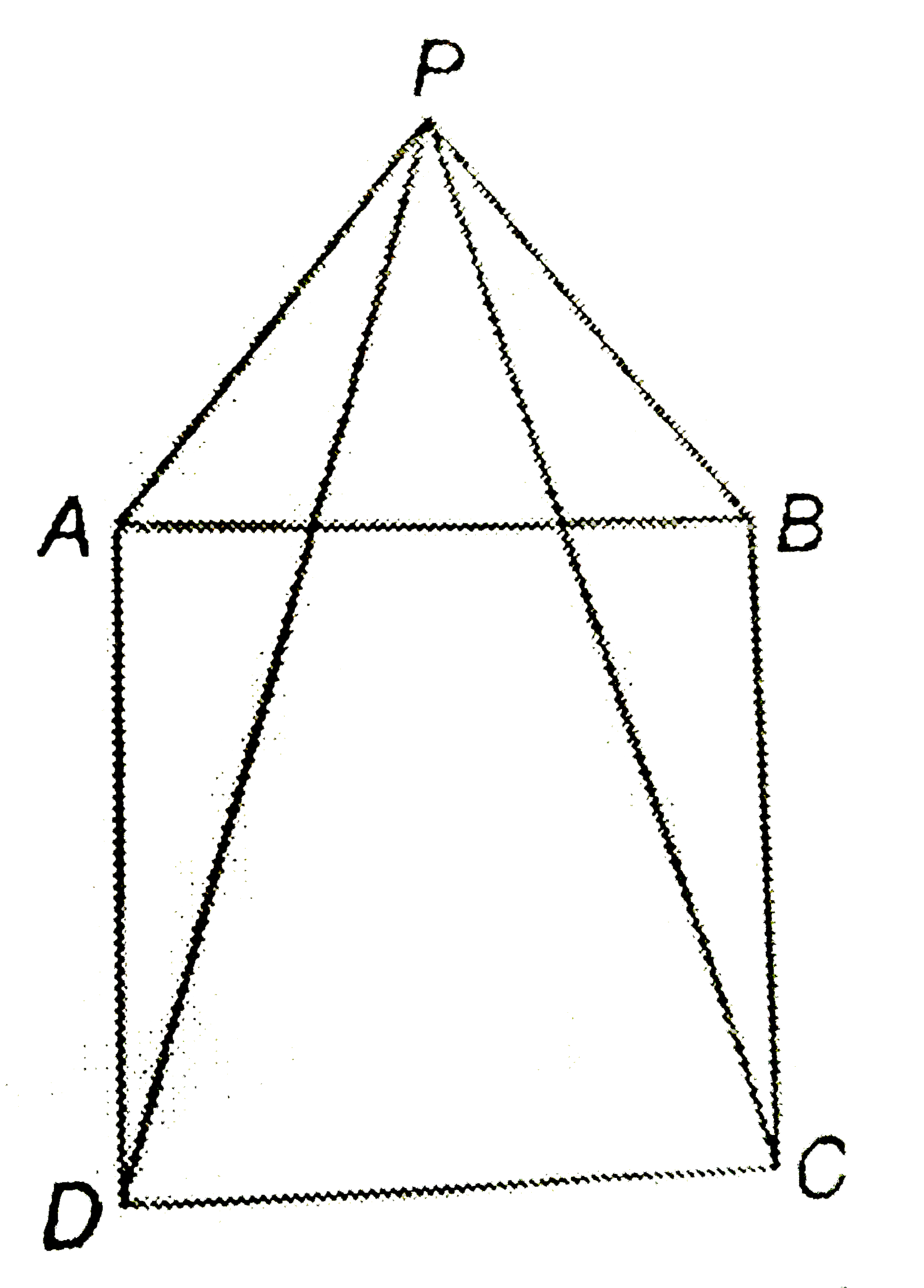
View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP
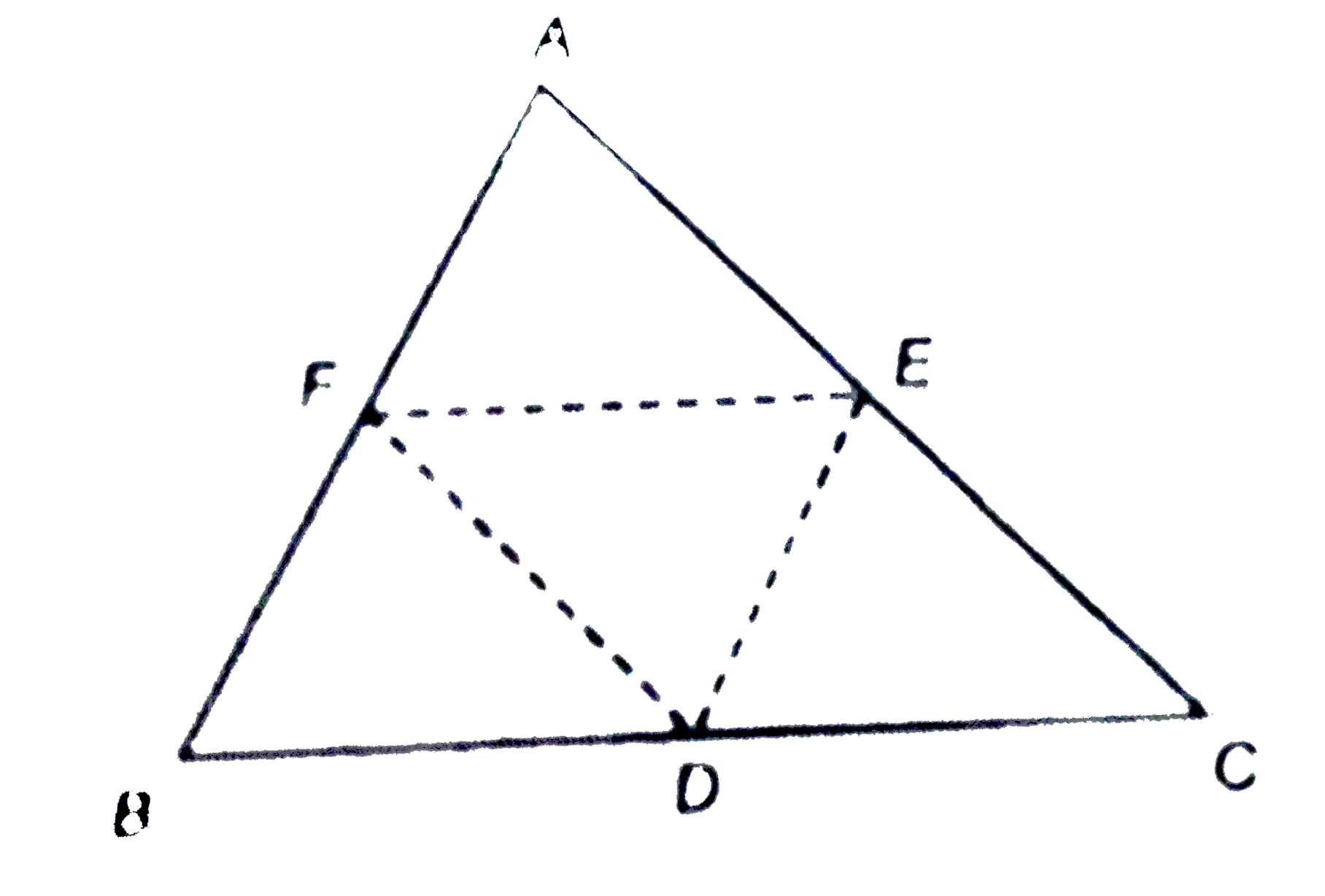
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC
View Solution
