Chords of a circle which are equidistant from the centre are equal.
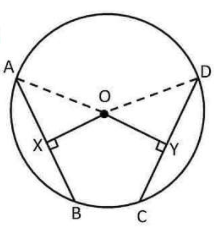
In △AOX and △DOY
∠OXA=∠OYD (perpendicular angles)
OA=OD (radius)
OX=OY (given)
By RHS congruency, △AOX and △DOY are congreunt.
AX=DY (CPCT)
For chord AB
OX⊥AB
Perpendiculars from center to chord bisects the chord.
AB=2AX
Similarly, for chord CD
CD=2DY
Thus,
AX=DY
2AY=2DY
AB=CD.
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.8
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.9
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.6
1 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- NUMBER SYSTEMSBOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
Equal chords of a circle are equidistant from the centre.
View SolutionProve Chords of congruent circles which are equidistant from the corresponding centres, are equal.
View SolutionPQ and RQ are chords of a circle equidistant from the centre. Prove that the diameter passing through Q bisects ∠PQR and ∠PSR
View SolutionEqual chords of congruent circles are equidistant from the corresponding centres.
View SolutionA chord of length 24 cm is at a distance of 5 cm form the centre of the circle. Find the length of another chord of circle which is at a distance of 12 cm from the centre.
View Solutionequal chords are equidistant from each other
View SolutionFrom the focus of the parabola y2=2px as centre, a circle is drawn so that a common chord of the curve is equidistant from the vertex and the focus. The radius of the circle is
View SolutionDescribe :
The locus of points within a circle that are equidistant from the end points of a given chord.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, then Prove chords are equal.
View SolutionTwo parallel chords of a circle, which are on the same side of centre,subtend angles of 72∘and144∘ respetively at the centre Prove that the perpendicular distance between the chords is half the radius of the circle.
View Solution
