Consider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the question:
Let PA=4 , PB=3 cm and CD is diameter of the circle having the length 8 cm. If PC>PD , then PCPD is equal to Solution in Punjabi
(a) 3
(b) 4
(c) 5
(d) 6
The correct Answer is:A
Step by step video & image solution for Consider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) . On the basis of above information , answer the question: Let PA=4 , PB=3 cm and CD is diameter of the circle having the length 8 cm. If PC gt PD , then (PC)/(PD) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - EXAMPLES ( Matching Type Questions )1videos
TRIGONOMETRIC EQUATIONS AND INEQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC EQUATIONS AND INEQUATIONSEXERCISE - EXAMPLES ( Subjective Type Examples )2videos
TRIGONOMETRIC EQUATIONS AND INEQUATIONS
- BOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam2videos
THREE DIMENSIONAL COORDINATE SYSTEM
- BOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)18videos
TRIGONOMETRIC FUNCTIONS AND IDENTITIES
Similar Questions
Find dydxiftan2x=siny
02:30View SolutionFind the solution of the equation (sinx+cosx)sin2x=a(sin3x+cos3x) located between π2 and π and for which values of 'a' does this equation have at most one solution satisfying the condition π2≤x≤π.
01:56View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
04:17View SolutionLet αandβ be non-zero real numbers such that 2(cosβ−cosα)+cosαcosβ=1. Then which of the following is/are true ?
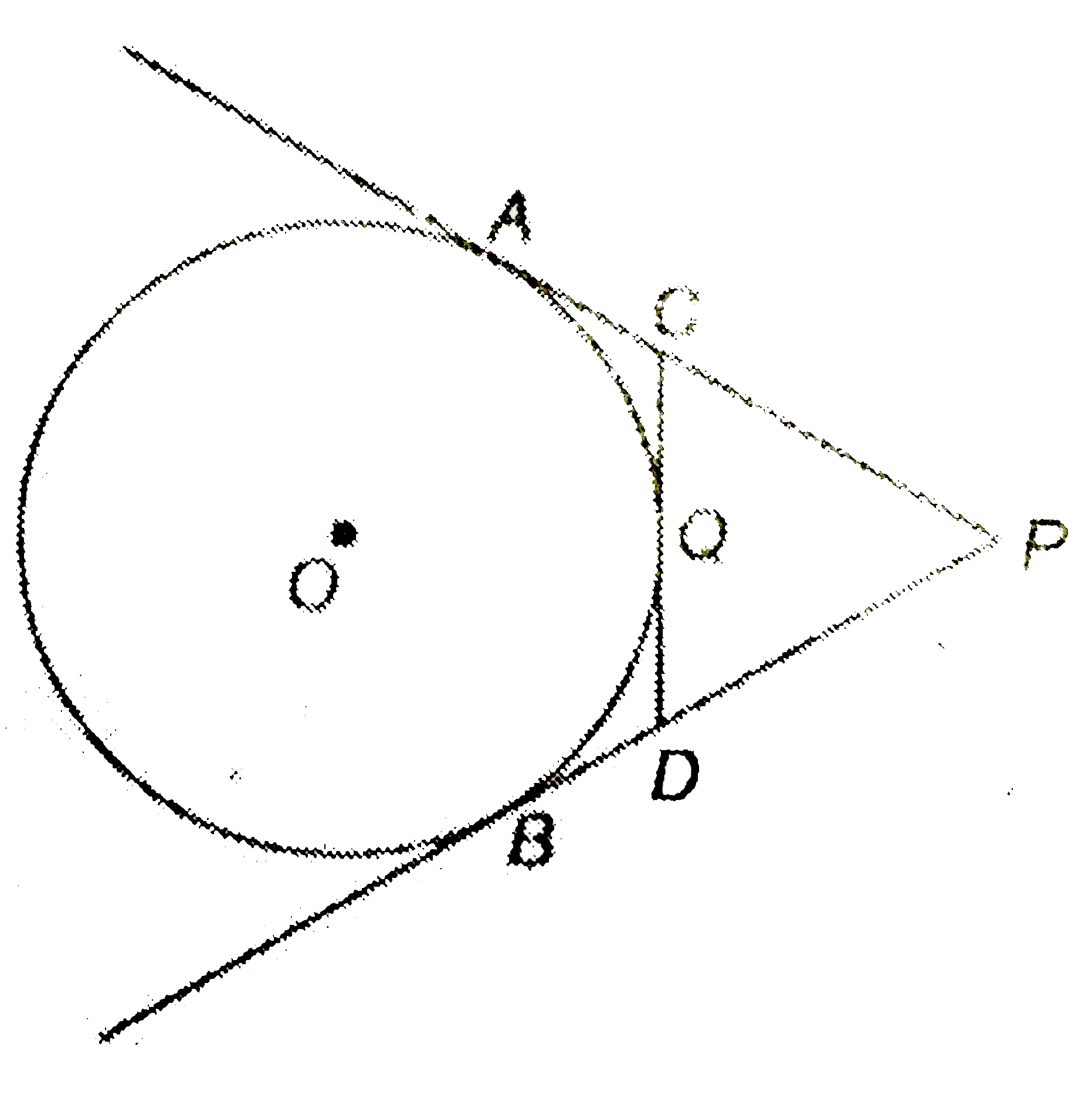
03:08View SolutionIn the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
 01:51View Solution
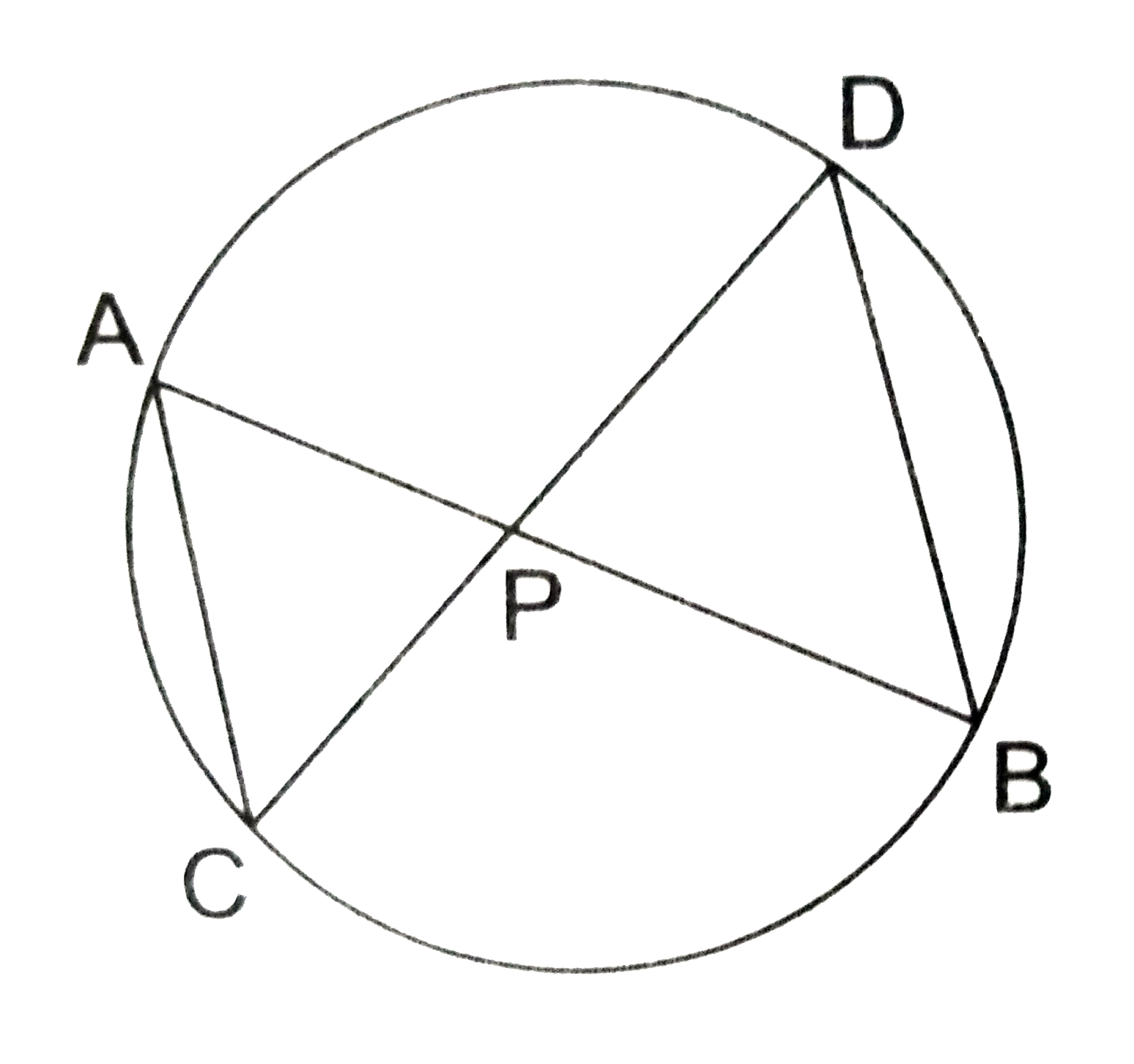
01:51View SolutionIn a cricle, two chords AB and CD intersect at a point P inside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
 02:02View Solution
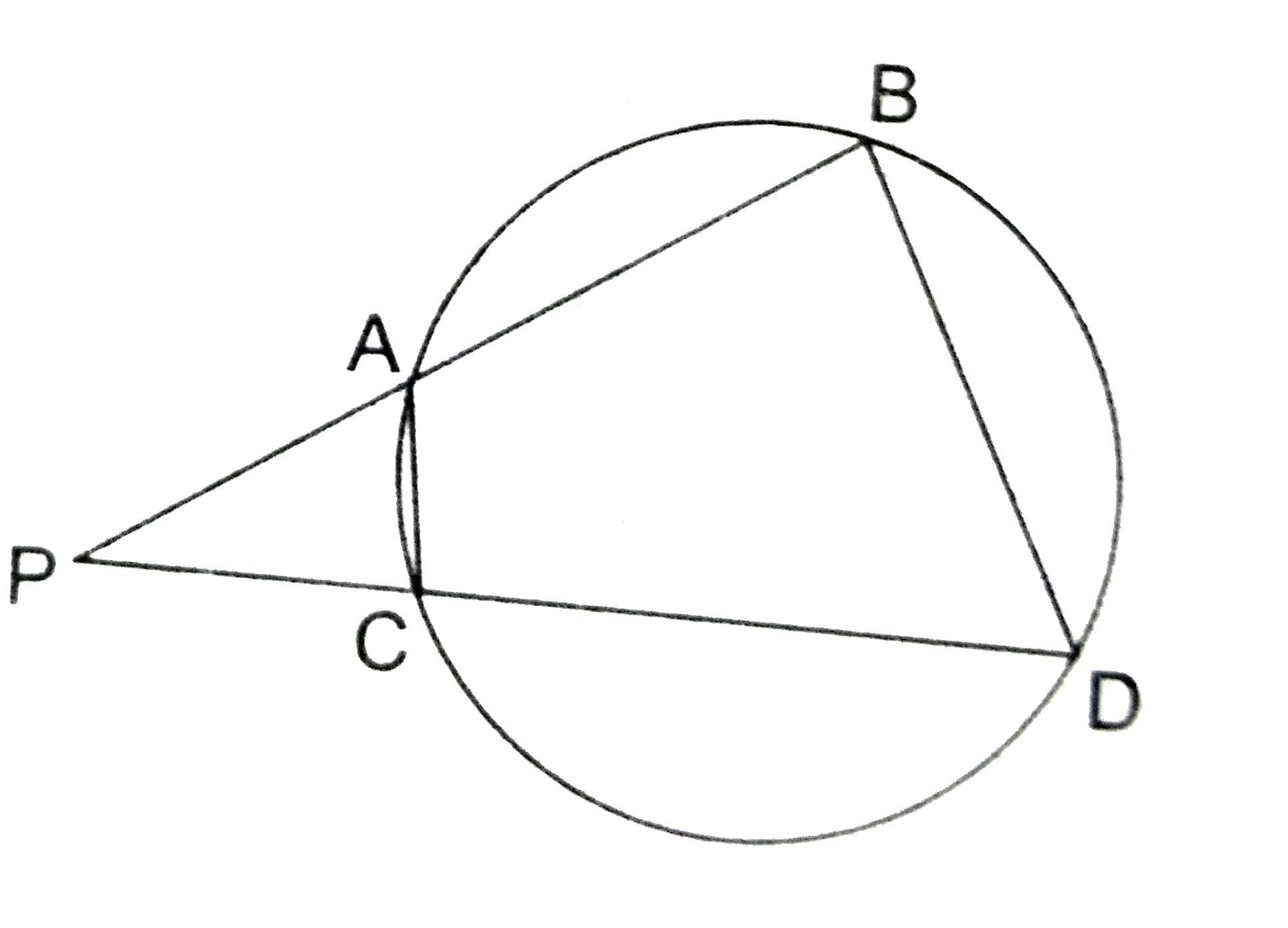
02:02View SolutionTwo chords AB and CD of a circle intersect at a point outside the circle. Prove that
(a)ΔPAC~ΔPDB (b)PA⋅PB=PC⋅PD.
 04:32View Solution
04:32View Solutionसंलग्न चित्र में, बाह्य बिन्दु P से दो स्पर्शी PA व PB हैं। CD एक दूसरी स्पर्शी हैं जो वृत्त को बिन्दु O पर स्पर्श करती हैं यदि PA = 12 सेमी, QC = QD = 3 सेमी तब PC + PD का मान ज्ञात कीजिए ।
07:29View SolutionConsider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the questions
If PA=|cosθ+sinθ|andPB=|cosθ−sinθ|, then maximum value of (PC)(PD) , is equal to01:48View SolutionConsider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the questions
If logPAx=2,logPBx=3,logxPC=4, then logPD x is equal to05:01View SolutionIn the given figure PA=6, PB=4 and PC=8. Find PD.
 02:23View Solution
02:23View SolutionIn the figure, a circle AB and CD j intersect at the P point on the outside of the circle, (i) trianglePAC ~ trianglePDB (ii) PA. PB = PC. Prove PD.
05:02View SolutionIn the given figure PA=6, PB=4 and PC=8. Find PD.
 03:46View Solution
03:46View SolutionIf chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
07:01View SolutionConsider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the questions
If PA=|cosθ+sinθ|andPB=|cosθ−sinθ|, then maximum value of (PC)(PD) , is equal to02:15View SolutionConsider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the questions
If logPAx=2,logPBx=3,logxPC=4, then logPD x is equal to04:19View Solution

