If chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
Step by step video & image solution for If chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA xx PB = PC xx PD . by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (E)
23 Videos
- PROBABILITYBOOK - ICSECHAPTER - PROBABILITYEXERCISE - EXERCISE 25(C)
106 Videos
Similar Questions
Two equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DP
View SolutionIn Figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that
(i) ΔPAC~ΔPDB
(ii) PA⋅PB = PC⋅PD

View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.

View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :
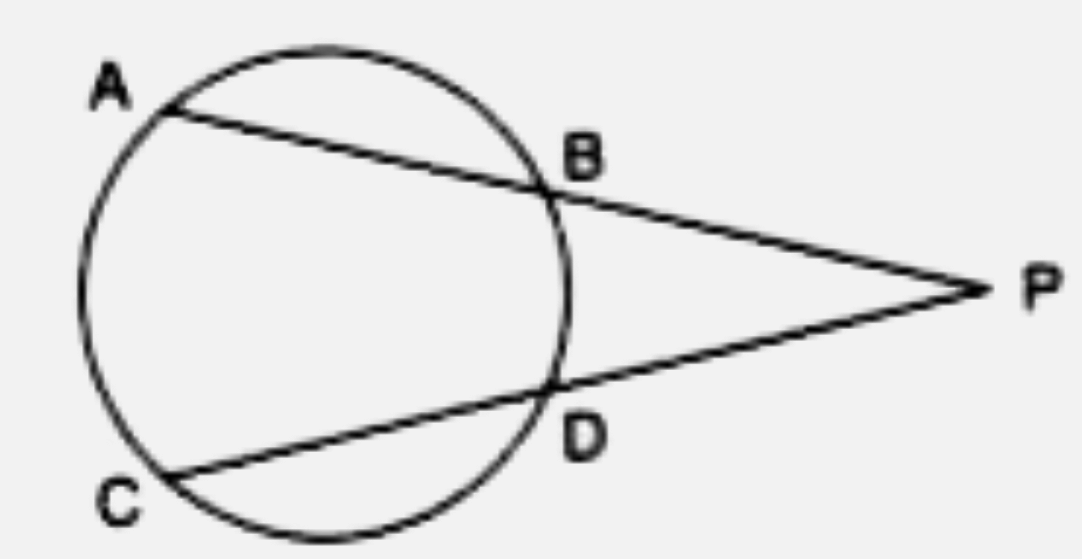
PA=PC.
View SolutionThe equal chords AB and CD of circle with centre O, when produced, meet at P outside the circle. Prove that :

PB=PD
View SolutionIn the adjoining figure, if chords AB and CD of the circle intesect each other at right angles, then find the value of x+y.
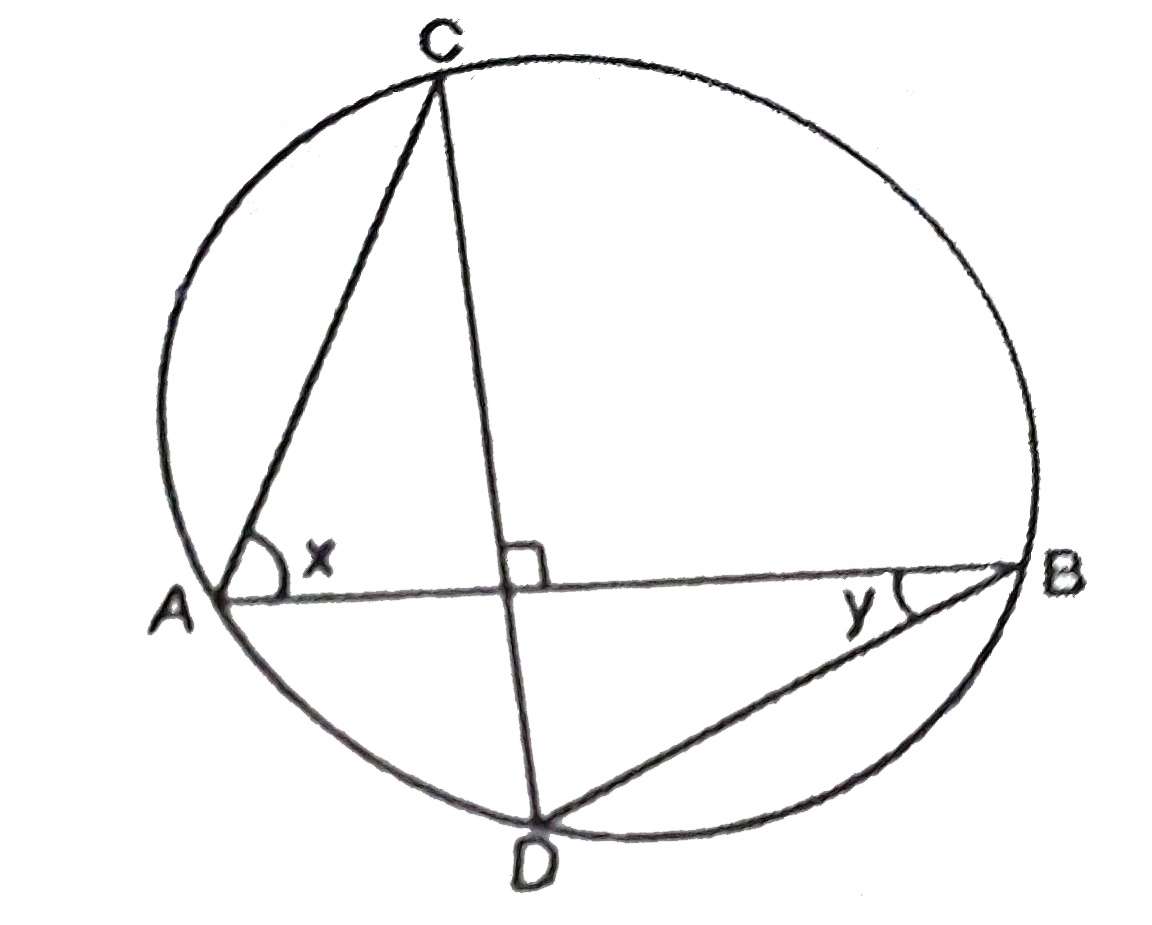
View SolutionTwo chords AB and CD of a circle are each at distances 4 cm from the centre. Then,
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
PA×PD=PB×PC.
View SolutionChords AB and CD of a circle with centre O, intersect at a point E. If OE bisects angle AED, prove that chord AB = chord CD.
View SolutionChords AB and CD of a circle are parallel to each other and lie on opposite sides of the centre of the circle. If AB = 36 cm, CD = 48 cm and the distance between the chords is 42 cm, find the radius of the circle.
View Solution
