Consider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The distance between the orthocenter and the circumcenter of triangle PQR is
25/2
29/2
37/2
51/2
The correct Answer is:A
Since the triangle is right-angled, the circumcenter is the midpoint of PQ and the orthocenter is R(1, -7). Hence,
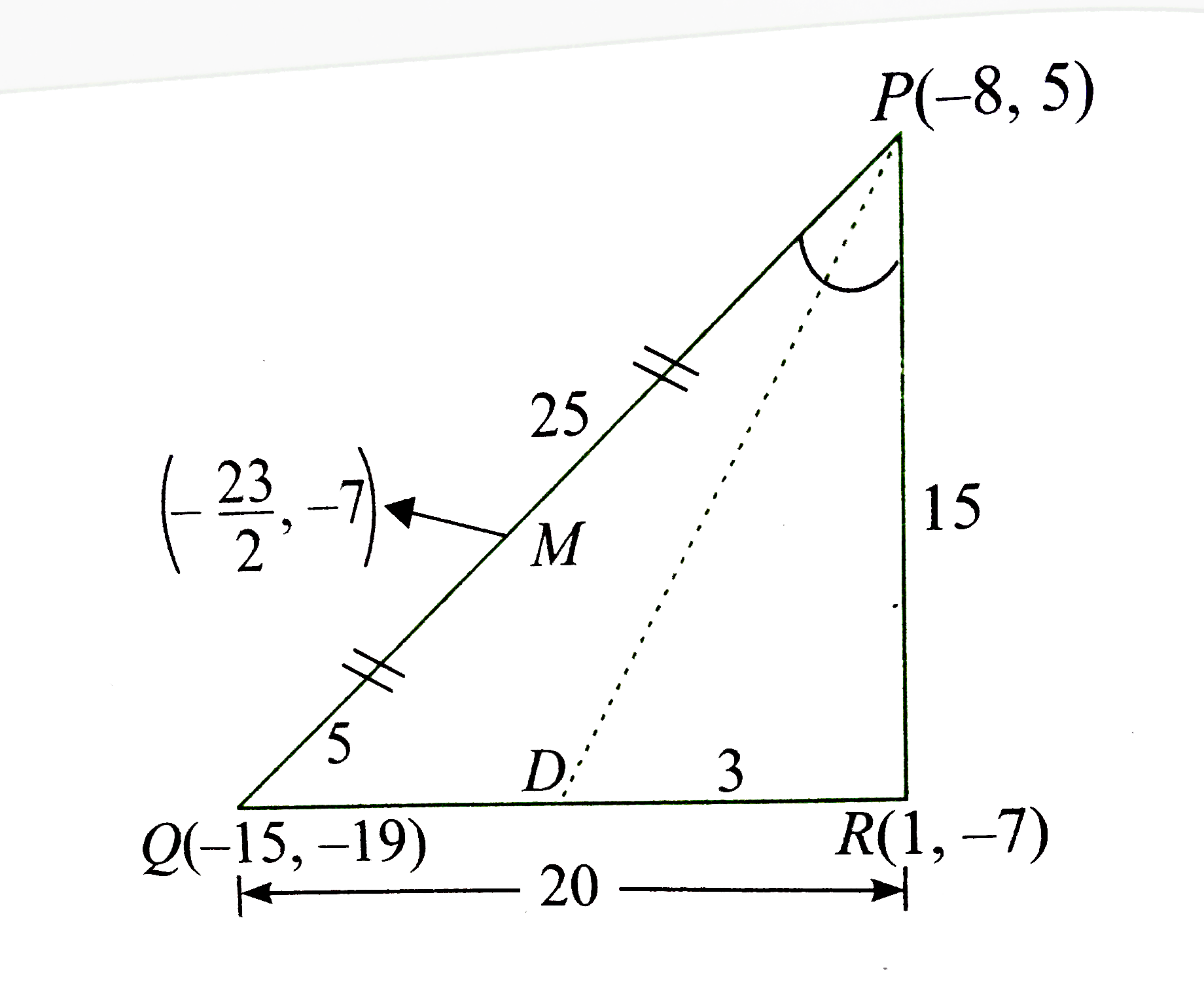
RM=∣∣
∣∣√(232+1)2∣∣
∣∣=1212
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Matrix)8videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Numerical)13videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise (Multiple)30videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider a triangle PQR with coordinates of its vertices as P(−8,5),Q(−15,−19), and R(1,−7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The radius of the in circle of triangle PQR isA4B5C6D8 - Question 2 - Select One
Consider a triangle PQR with coordinates of its vertices as P(-8,5), Q(-15, -19), and R (1, -7). The bisector of the interior angle of P has the equation which can be written in the form ax+2y+c=0.
The radius of the in circle of triangle PQR is
The sum a + c isA129B78C89Dnone of these - Question 3 - Select One
Consider a pair of perpendicular straight lines ax2+3xy−2y2−5x+5y+c=0.
Distance between the orthocenter and the circumcenter of triangle ABC isA4B9/2C8/3D7/4
Using integration, find the area of the triangle PQR, coordinates of whose vertices are P(2, 0), Q(4, 5) and R(6, 3).
View SolutionThe interior angle bisector of angle A for the triangle ABC whose coordinates of the vertices are A(−8,5),B(−15,−19)andC(1,−7) has the equation ax+2y+c=0 Find 'a' and 'c'
View SolutionIf the co - ordinate of the triangle P(4,3) Q(7,−1)andR(9,3) is then find the Area of triangle PQR and also find the types of triangle ?
View SolutionThe vertices of a triangle ABC are A(1,2),B(2.3) and C(3,1). Find the cosines of the interior angles of the triangle and hence or otherwise find the coordinates of, (a) orthocenter of the triangle(b) circumcentre of the triangle
View SolutionIf coordinates of the vertices of a triangle are (2,0), (6,0) and (1,5), then distance between its orthocentre and circumcentre is
View Solution

