Consider function f(x)=sin−1(sinx)+cos−1(cosx),x∈[0,2π]
(a) Draw the graph of y=f(x)
(b) Find the range of f(x)
(c) Find the area bounded by y=f(x) and x-axis
Video Solution
Text Solution
The correct Answer is:Range is [0,π], Area =π2 sq. units
f(x)=sin−1(sinx)+cos−1(cosx)
=x+x=2xx∈[0,π/2]=π−x+x=πx∈[π/2,π]=π−x+2π−x=3π−2xx∈[π,3π/2]=x−2π+2π−x=0x∈[3π/2,2π]
Graph of the function is as shown in the following figure
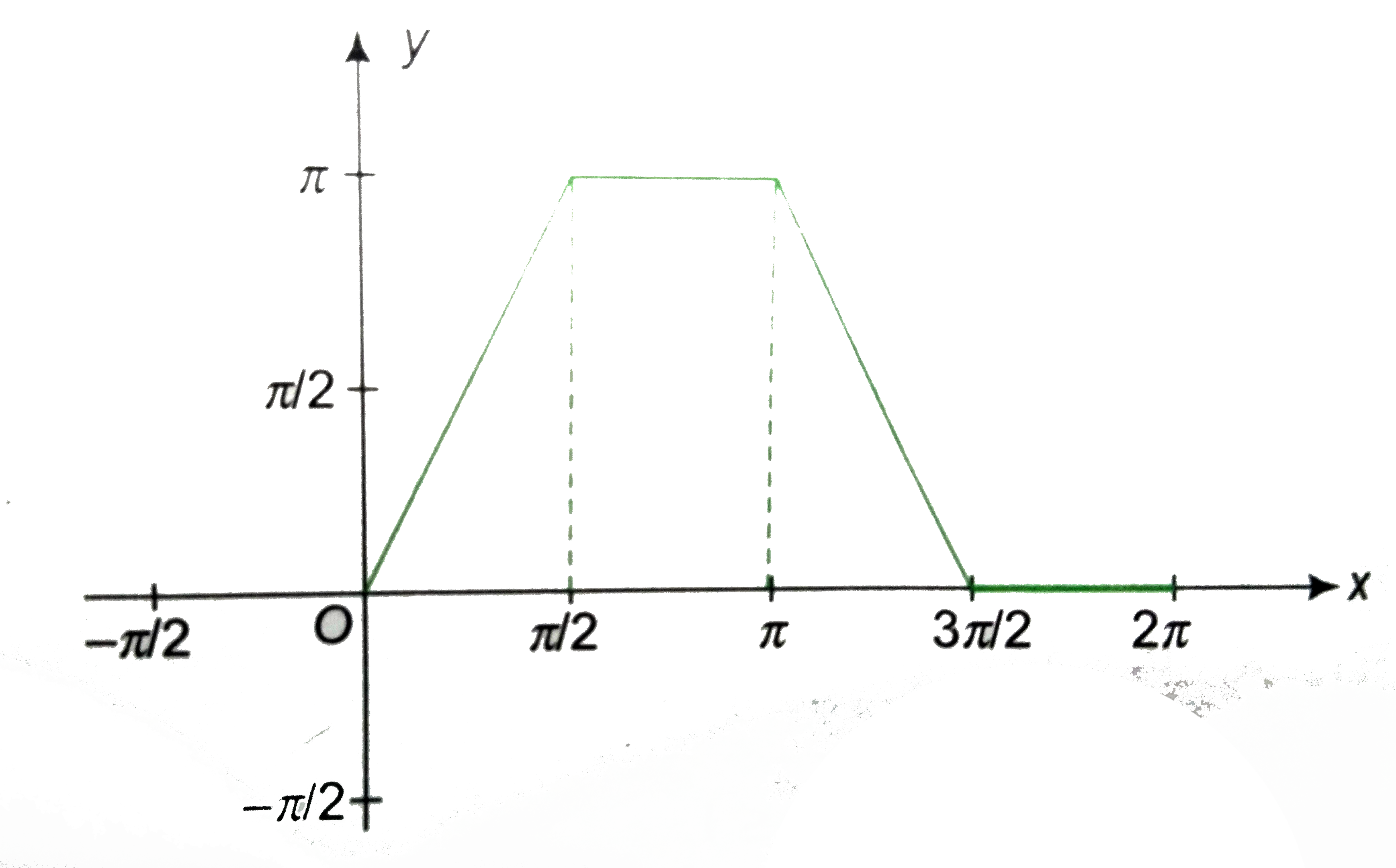
From the graph, rangle is [0,π]
Also, area bounded by y=f(x) and x -axis is,
A=12(3π2+π2)(π)
π2 sq. units
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.312videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.412videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Concept application exercise 7.112videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE3videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGE ENGLISHCHAPTER - JEE 2019EXERCISE - Chapter 109videos
JEE 2019
Similar Questions
The function f(x)=sin−1(cosx)is
View SolutionFind the area bounded by y = sin x and axis of x in (0,π)
View SolutionFind the range of f(x)=cos4x+sin2x−1.
View SolutionFind the range of f(x)=sin−1x+tan−1x+cos−1x
View SolutionFind the range of f(x)=(sin−1x)2+2πcos−1x+π2
View SolutionFind the domain of f(x)=sin−1x+cosx
View SolutionFind the area bounded by y=sin−1x,y=cos−1x ,and the X-axis.
View SolutionFind the range of f(x)=sin−1x+tan−1x+cos−1x.
View SolutionFind the range of the function f(x)=(sin−1x)3+(cos−1x)3.
View SolutionFind the area bounded by y=sin−1(sinx) and x-axis for x∈[0,100π]
View Solution

