Refer to the following diagram :

Column IColumn IIa.Collinear vectorsp.→ab.Coinitial vectorsq.→bc.Equal vectorsr.→cd.Unlike vectors (same initial point)s.→d
Text Solution
The correct Answer is:a→p,r,s;b→q,r,s;c→p,r;d→r,s

−−→AB=→a,−−→BC=→b ltvrgt ∴−−→AC=−−→AB+−−→BC=→a+→a (i)
−−→AD=2−−→BC=2→b (ii)
(because AD is parallel to BC and twice its length).
−−→CD=−−→AD−−−→AC=2→b−(→a+→b)
=→b−→a
−−→FA=−−−→CD=→a−→b (iii)
−−→DE=−−−→AB=−→a (iv)
−−→EF=−−−→BC=−→b (v)
−−→AE=−−→AD+−−→DE=2→b−→a (vi)
−−→CE=−−→CD+−−→DE=→b−→a−→a=→b−2→a (vii)
|
Topper's Solved these Questions
- INTRODUCTION TO VECTORS BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - TRUE OR FALSE
1 Videos
- INTEGRALSBOOK - CENGAGE ENGLISHCHAPTER - INTEGRALSEXERCISE - All Questions
764 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Numerical Value type)
2 Videos
Similar Questions
Knowledge Check
If the vectors →a,→b,→c,→d are any four vectors, then (→a×→b).(→c×→d) is equal to
A→a.{(b×(→c×→d)}B(→a.→c)(→b.→d)−(→a.→d)(→b.→c)C{(→a×→b)×→c}.→dD(−→dxx→c).(→b×→a)If the vectors →a,→b,→c and →d are coplanar vectors, then (→a×→b)×(→c×→d) is equal to
A→a+→b+→c+→dB→0C→a+→b=→c+→dDnone of theseLet →aand→b be two orthogonal unit vectors and →c is a vector such that →c×→b=→a−→c, then |→c| is equal to
A1B√2C1√2D2
Explain (i) Unit vector (ii) Equal vectors (iii) Negative vectors, (iv) Coinitial v ectors (v) Collinear vectors and (vi) Copanar vectors.
View SolutionColumn-I show vector diagram relating three vectors →a,→b and →c. Match the vector equation in column -II, with vector diagram in column-I:
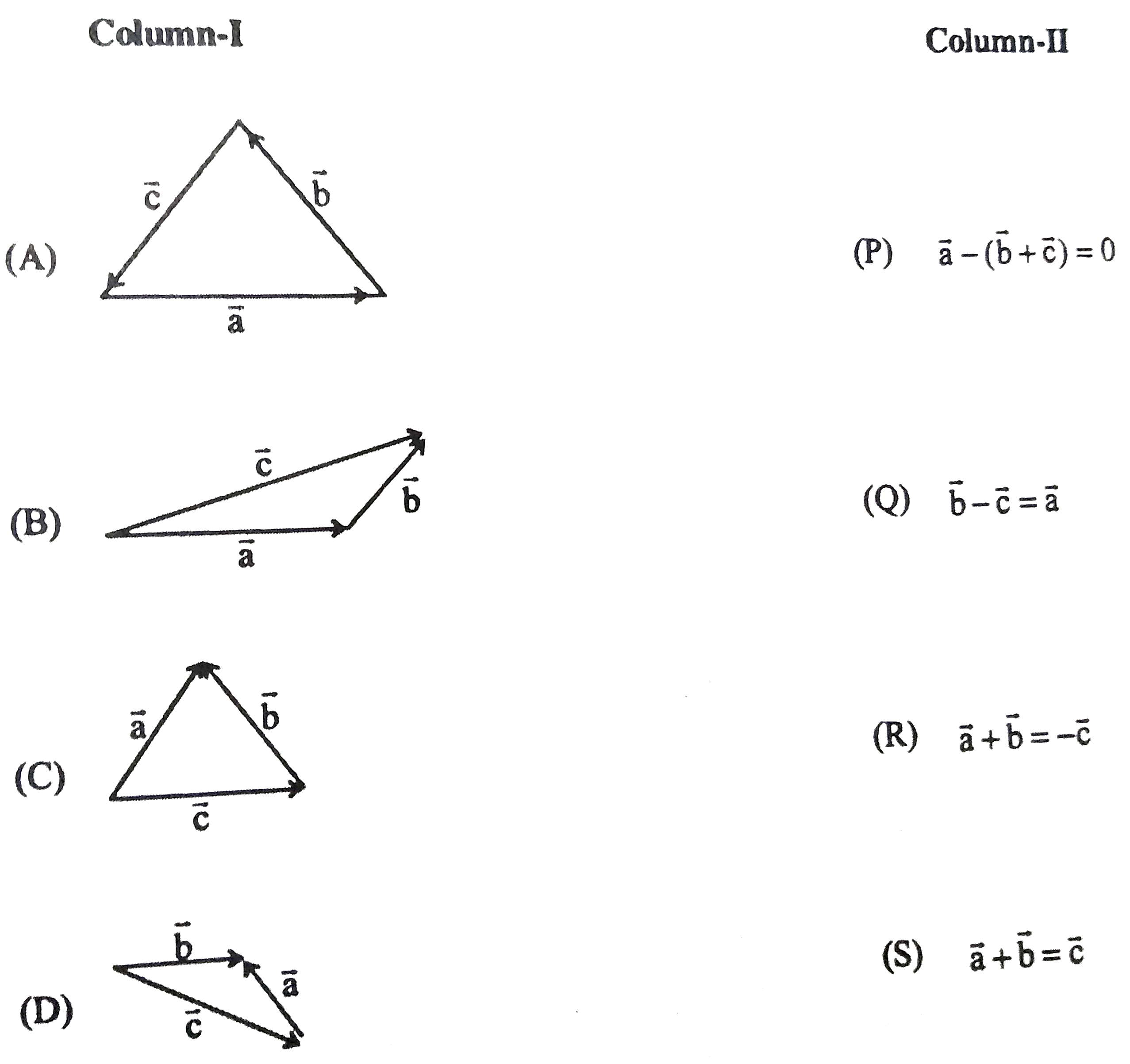
View SolutionColumn-I show vector diagram relating three vectors →a,→b and →c. Match the vector equation in column -II, with vector diagram in column-I:

View SolutionIf the vectors →a,→b,→c and →d are coplanar vectors, then (→a×→b)×(→c×→d) is equal to
View SolutionA, B, C and D have position vectors →a,→b,→cand→d, repectively, such that →a−→b=2(→d−→c). Then
View Solution
