Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
The maximum value of angle APB is

A

π3

B

π2

C

2π3

D

3π3

Text Solution
Verified by Experts

The correct Answer is:B

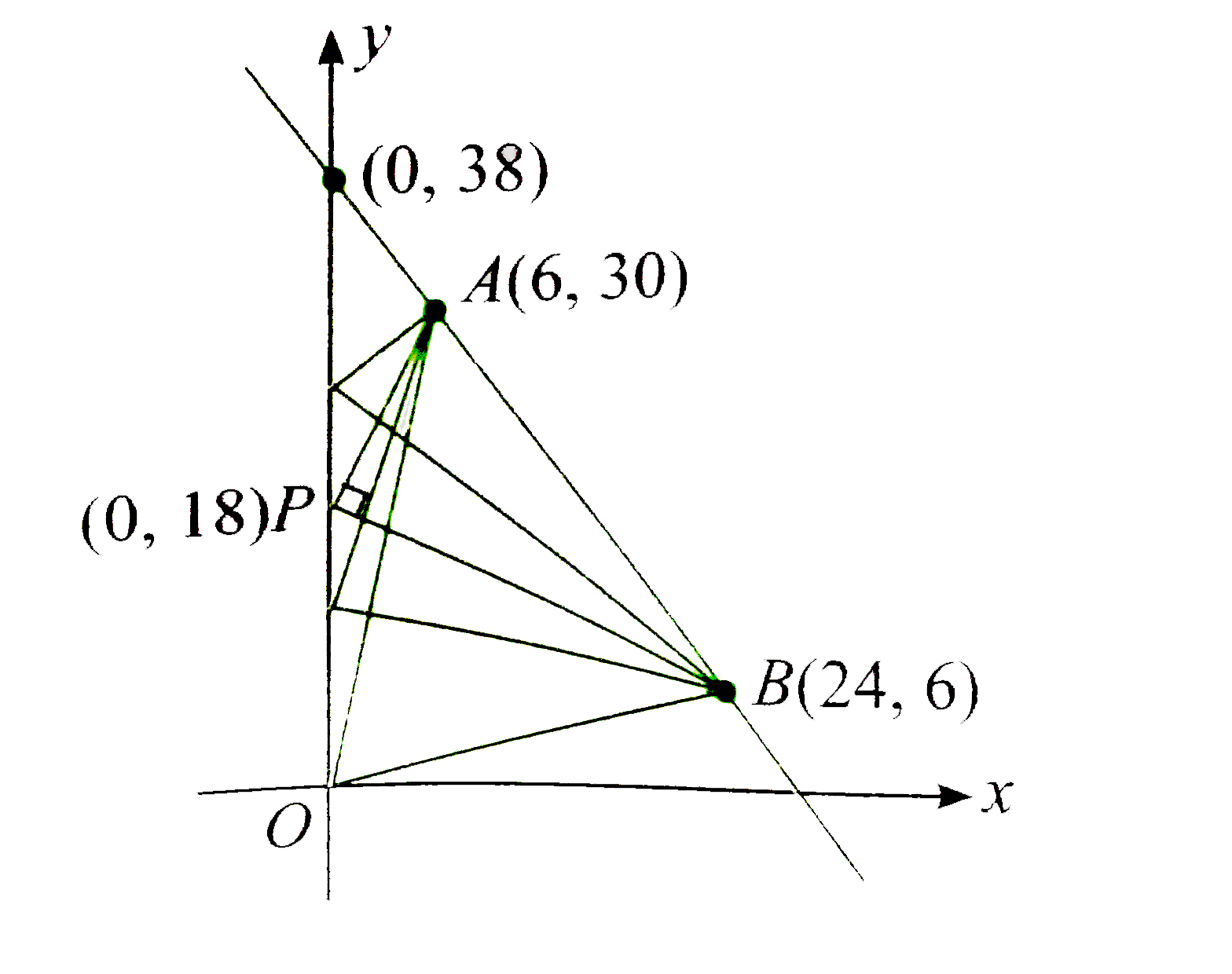
ocr_image
Slope of AP is m1=30−λ6
Slope of BP is m2=6−λ24
tanθ=30−λ6−6−λ241+(30−λ6)(6−λ24)
=720−24λ−36+6λ144+180−36λ+λ2
=18(38−λ)324−36λ+λ2=(38−λ)18(λ−18)2
Clearly, for 0<λ<38.
Maximum value of tanθ→∞ for which θ=π2,
Now, ddλ(tanθ)=18(18−λ)(λ−58)(λ−18)4
Clearly, λ=58 is point of maximum as derivative changes sign from '+' to '−'.
So, point Q≡(0,58) when ∠AQB is maximum.

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSSTRAIGHT LINES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
    Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
    For all positions of pont P, angle APB is maximum when point P is

    A(0, 12)
    B(0, 15)
    C(0, 18)
    D(0, 21)

  • Consider point A(6, 30), point B(24, 6) and line AB: 4x+3y = 114.
    Point P(0,λ) is a point on y-axis such that 0<λ<38 and point Q(0,λ) is a point on y-axis such that λ>38.
    For all positions of pont Q, and AQB is maximum when point Q is

    A(0, 54)
    B(0, 58)
    C(0, 60)
    D(0, 1)

  • Let two points be A(1,−1) and B(0,2). If a point P(x', y') be such that the area of ΔPAB=5 sq. units and it lies on the line, 3x+y−4λ=0, then a value of λ is:

    A4
    B1
    C−3
    D3